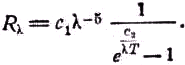 (5)
(5)[
вернуться к содержанию сайта]Формулы излучения Вина и Рэлея-Джинса
*). Есть некоторые физические законы, которые не могут быть выведены из ещё более фундаментальных положений. Они представляют собой обобщение экспериментальных результатов. К этому классу законов относятся первое и второе начала термодинамики, которые оба имеют всеобщее значение и весьма обширное поле приложения. Первое начало является хорошо известным законом сохранения энергии и его очень легко себе уяснить. Второе же начало, хотя оно также хорошо известно, осмыслить далеко не так легко. Дело в том, что вовсе не все процессы, не противоречащие закону сохранения энергии, действительно имеют место. Почему, например, если горячее тело привести в соприкосновение с холодным, оно не становится ещё более горячим, а холодное — ещё более холодным? Такой процесс не запрещается законом сохранения энергии. Причина его невозможности лежит в том, что хотя этот воображаемый процесс и согласуется с первым началом термодинамики, он нарушает второе начало, говорящее о направлении действительно совершающихся в природе процессов. Точная формулировка второго начала увела бы нас за пределы нашей темы, но мы можем высказать некоторые следствия, получающиеся в результате применения этого начала. Например:1) нельзя нагреть тело одним лишь приведением его в соприкосновение с более холодным;
2) нельзя перевести тепло от холодного тела к горячему, не совершая при этом механической работы.
Законы термодинамики были впервые успешно применены к вопросам излучения Вином в 1896 г. Вин искал соотношение, которое указывало бы, каким образом тепловое действие абсолютно чёрного тела меняется в зависимости от длины волны, т. е. искал уравнение, математически выражающее кривые, изображенные на рис. 24. Такое уравнение, в точности выражающее изменение кривой спектрального распределения энергии в зависимости от температуры, он получил. Он, например, смог предсказать кривую для 2000° К, если известна кривая для 1000° К. Это соотношение, известное под названием закона смещения Вина, является, несомненно, совершенно точным и представляет собой, вероятно, тот предел сведений о спектральном распределении энергии, которые мы можем получить, исходя из одних только законов термодинамики.
Однако закон смещения не может предсказать всей формы кривой для каждой данной температуры. Пытаясь получить соотношение, не страдающее этим недостатком, Вин сделал допущение, что существует известное сходство между излучением абсолютно чёрного тела и идеальным газом, в частности, что максвелловский закон распределения скоростей молекул даёт также и распределение лучистой энергии по длинам волн. Он получил следующее уравнение для количества энергии
Rλ длины волны λ, излучаемой с единицы поверхности:R
λ =c1λ–5/ec2/λT. (3)Здесь е
— основание натуральных логарифмов, равное 2,718, а с1 и с2 — константы. Эта формула согласуется с законом четвёртой степени. Как мы увидим позже, она хорошо согласуется с действительностью в области коротких волн, а именно в видимой области, но оказывается несостоятельной в области длинных инфракрасных волн.Вскоре после этого, в 1900 г., лорд Рэлей заметил некоторую несогласованность результатов, получающихся при применении максвел-ловского закона распределения. Тогда он пришёл к предположению о применимости другого, весьма важного при изучении газов соотношения, а именно — закона равномерного распределения энергии по различным степеням свободы. Удобной иллюстрацией здесь является скрипичная струна, способная совершать колебания самого различного вида. В одно и то же время она может давать не только основной тон, но и гармонические обертоны. Частоты испускаемых колебаний соответствуют вибрациям струны как целого, струны, разделённой на две части, на три части и т. д. Мы можем считать эти виды колебаний степенями свободы и полагать, что с основной частотой, а также с каждым обертоном сопряжено по одной степени свободы. Если бы для такой вибрирующей струны оправдывался закон распределения энергии, то мы обнаружили бы, что энергии основного колебания, а также первого, второго и следующих обертонов равны между собой. Конечно, это не имеет места в случае скрипичной струны, возбуждаемой смычком обычным способом. Однако Рэлей допустил возможность таких условий для лучистой энергии, возникающей в полости абсолютно чёрного тела. Его формула, представленная
в более простом виде и теоретически лучше обоснованная Джинсом, имеет следующий вид:R
λ =c3λ–5f(λ, T). (4)Здесь
c3 — константа, а f(λ, T) — универсальная функция λ и Т. Эта формула согласуется с законом смещения Вина, но не согласуется с законом четвёртой степени. В противоположность формуле Вина она оказывается несостоятельной в области коротких длин волн, но точно выражает действительное положение вещей для очень длинных инфракрасных лучей.Формула излучения Планка. Положение, которое в 1900 г. застал Планк, характеризовалось двумя, по-видимому, хорошо обоснованными соотношениями для спектрального распределения энергии излучения абсолютно чёрного тела, а именно соотношениями Вина и Рэлея. Оба были правильны с точки зрения термодинамики. Оба частично основывались на принципах классической механики. Оба в некоторой части находились в согласии с опытом, а частью ему противоречили, причём одно соблюдалось там, где другое оказывалось неудачным. Классическая физика казалась беспомощной и не могла уже идти дальше.
Пытаясь уяснить причины неудачи, Планк заметил, что формула, которую он получил, стараясь оправдать формулы (3) и (4), предсказывала значения, согласные с формулой Вина, там, где она оказывалась верной, и с формулой Рэлея, где эта последняя была правильна. Эта формула такова:
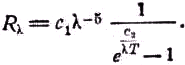 (5)
(5)
Здесь
c1 и c2 — константы. Эта формула согласуется с законом четвёртой степени Стефана-Больцмана, т.е. формулой (2), а также с законом смещения Вина. Далее, когда ec2/λT велико по сравнению с единицей (например для малых значений произведения λT), она сводится к формуле Вина, а когда эта величина мала и сравнима с единицей — к формуле Рэлея-Джинса. Рис. 25 показывает, насколько формула Планка согласуется с экспериментом и как она в предельном случае переходит в формулы Вина и Рэлея-Джинса.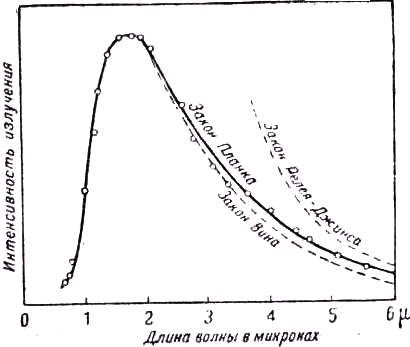
Рис. 25. Кривая распределения энергии в спектре излучения абсолютно чёрного тела по измерениям Кобленца, а также кривые, получаемые на основе формул Вина, Рэлея-Джинса и Планка.
Имея правильное выражение для
Rλ как функции λ, Планк стал искать для него физическое объяснение. В результате этих поисков появилась идея квантов.Классическая механика представляла себе процесс испускания и поглощения лучистой энергии первичным источником (атомами или молекулами, образующими излучающее тело), происходящим постепенно и совершенно произвольно. Изменение со временем энергии элементарного атомного источника, находящегося среди огромного числа ему подобных, представлялось происходящим так, как это показано на рис. 26. Промежутки, на которых кривая содержания энергии поднимается вверх, являются периодами поглощения энергии. Интервалы, на которых имеется наклон вниз, выражают периоды испускания энергии. Отказываясь от традиционных представлений, Планк сделал смелое предположение, приняв, что первичный источник испускает лучистую энергию не непрерывно, а прерывисто, и притом, что ещё более важно, пакетами или, как их часто называют, квантами, содержащими вполне определённое количество энергии. Предполагается, что после вылета они имеют определённую волновую структуру с частотой ν и содержат количество энергии ε, даваемое соотношением:
ε=
hν=hc/λ, (6)где с — скорость света и
h — множитель пропорциональности. Только таким образом Планк смог обосновать уравнение (5). С этой точки зрения изменение в зависимости от времени энергии, содержащейся в идеализированном элементарном атомном источнике, способном испускать и поглощать энергию только одной определённой частоты, выражается прерывистым графиком, показанным на рис. 27. В том случае, когда источник способен испускать излучение более чем одной частоты, положение оказывается более сложным, но всё же аналогичным описанному.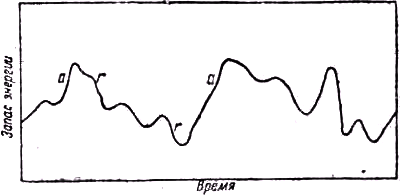
Рис.
26. График предполагаемого изменения со временем количества энергии, содержащейся в первичном элементарном источнике излучения, согласно классической теории. Периоды поглощения энергии обозначены буквой а, периоды излучения энергии — буквой r.
Рис. 27. График предполагаемого изменения со временем количества энергии, содержащейся в первичном элементарном источнике излучения, согласно квантовой теории для случая, когда возможно испускание энергии лишь одной какой-нибудь частоты. Моменты поглощения энергии обозначены буквой а, моменты испускания — буквой
r. Длительность интервалов, в течение которых источник обладает энергией, сильно преувеличена. Этот график в большей степени соответствует впоследствии развившимся квантовым представлениям, чем первоначальной точке зрения Планка.Константы уравнения (5)
c1 и c2 не являются вполне независимыми. Кроме того, они относятся не только к излучению абсолютно чёрного тела и не должны быть обязательно определяемы экспериментально. Они связываются между собой и с прочими отделами физики через посредство скорости света и больцмановской постоянной k. Вставляя эти величины, мы можем переписать уравнение (5) в таком виде: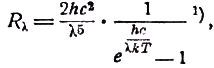
где встречается только одна новая постоянная
h. Но так как в настоящее время эта постоянная h встречается почти во всех теоретических рассуждениях, её можно рассматривать как постоянную, связывающую это уравнение с уравнениями других отделов физики. И её, действительно, надо рассматривать как универсальную постоянную, важность которой можно сравнить лишь с важностью гравитационной постоянной или величины скорости света в пустоте.Значение
h можно вычислить, комбинируя экспериментально полученное значение для с2 из уравнения (5), равное 1,4317 см·град., с указанными уже ранее экспериментальными же значениями k и с. Приравнивая показатели при е в формулах (5) и (7) и подставляя эти значения, мы получим: (8)
(8)
Другое независимое определение описывается в следующем разделе этой главы в связи с рассмотрением несколько изменённой точки зрения, развивавшейся из работы Планка о спектре абсолютно чёрного тела. Перед тем как идти дальше, мы должны подчеркнуть следующие три положения:
1) Планк в своей теории интересовался прежде всего процессом испускания излучения.
2) Хотя он пришёл к постулированию корпускулярности испускания лучистой энергии, идеи корпускулярного распространения ещё не требовалось.
3) Идея корпускулярного распространения укрепилась лишь в результате приложения квантовых идей к рассмотрению фотоэлектрического эффекта, который мы изложим в следующем разделе.
Для объяснения наблюдаемых при опытах атомных спектров физик вынужден обратиться к подробному рассмотрению движения внеядерных электронов и исходя из него строить, если пользоваться языком теории Бора, сложную систему круговых и эллиптических орбит, соответствующих различным значениям энергии. С другой стороны, химик больше интересуется возможным поведением двух различных атомов, чем внутренним движением, происходящим внутри каждого из них в отдельности. Задача химика может считаться почти решённой, если он сумел объяснить химическое соединение и процесс образования молекул. Атом Резерфорда-Бора с его непрерывным движением электронов по опоясывающим ядро орбитам излишне сложен для химика, удовлетворявшегося вплоть до последнего времени рассмотрением статической модели, в которой электроны считаются покоящимися. Это упрощение оправдывалось тем, что оно приводило к рациональному объяснению валентности и образования химических соединений. Разумеется, химик не думал при этом, что статическая модель является правильным отображением истинной природы атома. Она являлась просто удобным инструментом для предсказывания тех явлений, которые его больше всего интересовали.
|
Не |
Ne |
Ar |
Кг |
Хе |
Rn |
|
2 2(1) |
10 2 (1 + 22) |
18 2 (1 + 22 + 22) |
26 2 (1+22+ + 22 + 32) |
54 2 (1+22+22+ + 32 + 32) |
86 2 (1+22+22+ +32 + 32 + 42) |
Число электронов, окружающих ядро атома благородного газа, обнаруживает замечательный закон возрастания, который показан на приводимой выше таблице.
Одним из самых интересных свойств атомов этих элементов является их неспособность образовывать соединения ни с атомами того же самого типа, ни с другими атомами. Очевидно вообще, если порядковый номер элемента может быть написан в виде выражения, составленного по образцу одной из колонок этой таблицы, то данный элемент является необычайно устойчивым. Перечисленные шесть элементов являются единственными элементами, не вступающими ни в какие химические соединения. Поэтому представляется весьма правдоподобным предположение, что внеядерные электроны размещены по оболочкам, каждая из которых содержит 2n2
электронов, где п может принимать последовательные целые значения — 1, 2, 3 и 4. Так, принято считать, что в Kr два электрона (2·12) расположены ближе к ядру, чем другие. Далее по направлению к периферии от них находится группа из восьми электронов (2·22); затем идут группы из восьми (2·22) и восемнадцати (2·32) электронов.Льюис предложил считать, что атомы действительно содержат такого рода концентрические электронные оболочки, и следующие друг за другом по мере возрастания порядкового номера элементы образуются благодаря происходящему каждый раз добавлению одного нового электрона. Так, неон, у которого имеется 10 электронов, содержит две законченные
оболочки, состоящие соответственно из двух и восьми электронов. Добавление ещё одного электрона (сопровождающееся одновременным изменением ядра) дало бы нам атом натрия, который также содержит две законченные оболочки, но, кроме того, имеет ещё один электрон, находящийся на сравнительно большом расстоянии вне второй оболочки. Продолжая таким образом дальше, мы получим модели магния, алюминия, кремния, фосфора, серы и хлора. В этом последнем элементе на строящейся третьей оболочке имеется уже семь электронов. Прибавим теперь ещё один электрон. Тогда оболочка заполнится, и мы получим инертный газ аргон. Лэнгмюр заметил, что в случае атомов с низким атомным весом эти восьмерные группы (октеты) очень удобно изображать, размещая электроны в вершинах куба, в центре которого расположено ядро. Для пояснения этой точки зрения мы приводим рис. 101, на котором изображена такая атомная модель Льюиса-Лэнгмюра для фтора (9), неона (10) и натрия (11).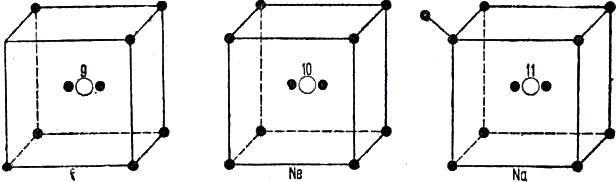
Рис. 101. Льюис-лэнгмюровская модель фтора, неона и натрия.
Здесь ясно видно, что фтору не хватает всего одного электрона, чтобы завершить восьмерную группу и дать очень устойчивое образование. Нет поэтому ничего удивительного в том, что этот элемент очень легко образует одновалентный отрицательный ион F–. С другой стороны, натрий сверх завершённой восьмерной группы имеет один электрон, который он легко теряет, образуя одновалентный положительный ион Na+. Таким путём низкий ионизационный потенциал натрия (5,13 V), о котором мы говорили выше, получает весьма правдоподобное объяснение. Неон, имеющий завершённую восьмерную группу, стоит между фтором и натрием. Невысокий уровень его точек плавления и кипения есть лишь результат слабости его связи с другими атомами. С другой стороны, его упорное стремление сохранять полное количество электронов, свойственных ему в нормальном состоянии, проявляется в высоком ионизационном потенциале (21,5 V).
Лэнгмюровская теория восьмерных групп даёт нам также и механическую картину образования молекул. Так как фтор стремится принять на себя один электрон, а натрий потерять, то они легко соединяются вместе, образуя
NaF, устойчивость которого объясняется электростатическим притяжением положительного и отрицательного ионов. В качестве иллюстрации дальнейшего распространения этой теории мы приводим на рис. 102 льюис-лэнгмюровские модели для молекул F2 и О2. В первом случае два куба имеют одно общее ребро, благодаря чему восьмерные группы становятся завершёнными. Тот факт, что в осуществлении этой связи принимают участие два электрона, соответствует однократной химической связи. В молекуле же О2 два куба имеют общую грань, чему соответствует наличие двойной связи.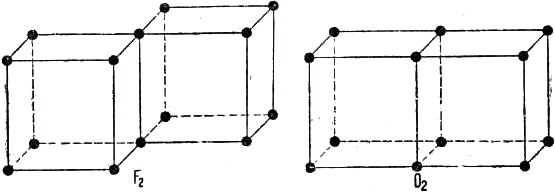
Рис. 102. Модели молекул фтора и кислорода.
Мы потому так подробно останавливаемся на разборе этой довольно устаревшей теории, что она благодаря своей простоте даёт нам возможность весьма наглядного мысленного представления всей картины. Атомная модель Бора-Резерфорда, принятая физиками, имеет то общее с моделью Льюиса и Лэнгмюра, что она также основывается на размещении электронов по оболочкам. Однако здесь отдельные электроны уже не находятся в покое, а движутся по эллиптическим или круговым орбитам, причём все электроны одной оболочки находятся приблизительно на одинаковых расстояниях от ядра. Объяснение химических свойств элементов с помощью такой динамической модели наталкивается на значительные трудности. Однако мы можем и здесь достичь успеха, если откажемся от механической модели, предлагаемой Бором, и обратимся к идеям волновой механики, которые несмотря на их меньшую наглядность обладают не меньшей определённостью.
*) Более подробное изложение математической стороны вопроса см. Лоренц, Лекции по теоретической физике, I. Теория излучения. ОНТИ, М.—Л. 1935. (Прим, перев.)
) Это соотношение можно выразить по иному, а именно: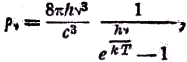
где ρ
ν выражает плотность излучения, распространяющегося с частотой ν.Дата установки:
24.02.2008