[вернуться к содержанию сайта]
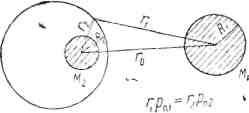
Пусть имеются два неподвижных сферических тела, массы которых М1 и М2, находящихся на расстоянии r0 друг от друга. Газ, испускаемый телами, будем считать ультрарелятивистским, уравнение состояния газа пусть будет
pv = RT, (1)
где R= const. Уравнение адиабаты pv4/3= const, причем р=ρс2/3. Можно приближённо допустить, что давление газа, истекающего из одного тела, будет падать до какого-то давления внешней среды, определяемого также потоком газа, истекающего из другого тела (см. рис. 1). Очевидно, что
r12 = r22+ r02 - 2r0r2 cos φ cos λ, (2)
где φ — “широта” и λ — “долгота” относительно второго тела заданной точки, находящейся на расстоянии r1 от первого тела и на расстоянии r2 от второго тела.

Рис. 1
Если r0>>R1 и r0>> R2, где R1 и R2 — радиусы тел М1 и М2, то, как известно (1),
![]() (3)
(3)
где ![]() - масса газа, испускаемого телом М2; р02, v02 — давление и удельный объём газа в теле М2. Принимая k= 4/3, получим
- масса газа, испускаемого телом М2; р02, v02 — давление и удельный объём газа в теле М2. Принимая k= 4/3, получим
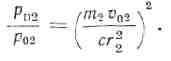 (4)
(4)
Аналогично для тела М1 будем иметь
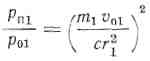 . (5)
. (5)
Отсюда следует, что сила давления и пропорциональная ей сила реакции F~ т2/r2 (если k≠ 4/3, то этот закон уже не будет иметь места).
Когда газ можно рассматривать как сплошную среду, то истечение из обоих тел будет происходить до тех пор, пока не выровняются давления, т. е. пока не будет выполняться условие
pп1 = pп2, (6)
где pп1 и pп2 — давления газа соответственно для первого и второго тела. Однако, если учитывать боковое перетекание газа, то истечение будет происходить до тех пор, пока на каждой элементарной площадке не уравняются действующие силы ![]() При этом в среднем должно выполняться условие вида
При этом в среднем должно выполняться условие вида
pп1 r12 = pп2 r22 (7)
Если истекают разреженные газы, то нужно учесть глубину их взаимного проникновения. При этом взаимодействие тел несколько уменьшится.
На основании (4) и (5) имеет место соотношение m12 p01 v012/r12= m22 p02 v022/r22pп2 r22 или на основании (1), принимая, что температура Т0= const, ![]()
Исключая r12 из (2) с помощью (6), пренебрегая боковым перетеканием газа, которое несущественно, придём к уравнению поверхности, на которой ![]() откуда
откуда
![]()
Известно (1), что если r0>>R, то скорость истечения
![]() (8)
(8)
это выражение для тела М2 при k= 4/3 имеет вид
![]() (9)
(9)
Поскольку масса газа, истекающая через элементарную площадку df =r2 cosφdφdλ, есть ![]() , то проекция силы, действующей на тело М2, на ось r0 есть
, то проекция силы, действующей на тело М2, на ось r0 есть
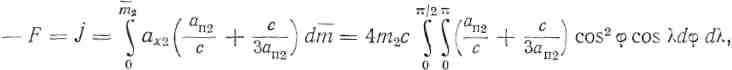 (10)
(10)
где ах2 = а2 cos φ cos λ.
(11)
Подставляя сюда ап2 из (9), придём к выражению ![]() где
где
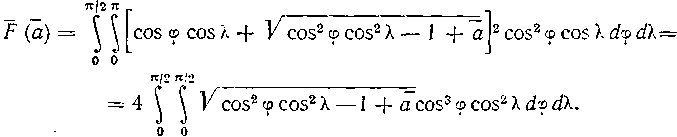 (11)
(11)
В общем виде ![]() вычислить затруднительно. Если
вычислить затруднительно. Если ![]() , что может иметь место при M1/M2>1 и, следовательно, при
, что может иметь место при M1/M2>1 и, следовательно, при ![]() , то
, то
![]() (12)
(12)
При этом
![]() (13)
(13)
Если ![]() , то будут иметь место соотношения
, то будут иметь место соотношения
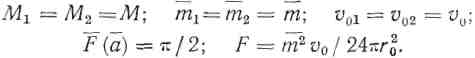 (14)
(14)
Если в (13) положить ![]() , то получим
, то получим
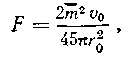 (15)
(15)
что мало отличается от (14). Таким образом, вычисляя ![]() , достаточно ограничиться первым членом разложения в ряд по степеням
, достаточно ограничиться первым членом разложения в ряд по степеням ![]() и считать, что можно провести исследование при помощи интерполяционного соотношения, дающего правильные результаты для
и считать, что можно провести исследование при помощи интерполяционного соотношения, дающего правильные результаты для ![]() → ∞ и
→ ∞ и ![]() = 1:
= 1:
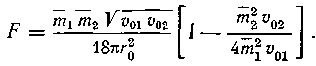 (16)
(16)
При ![]()
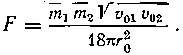 (17)
(17)
Очевидно, что сила взаимодействия между телами будет силой притяжения, поскольку газ расширяется неравномерно, а именно, меньше при истечении в область внутри тел. При этом разность количеств движения истекающего газа и приведёт к “притяжению” тел. На тела действует также сила давления Fp, однако, поскольку Fp ~ ρR2, a F~ ρr02, то Fp/F~ R2/r02, откуда следует, что силой давления при R/r0>1 можно пренебречь.
Случай M1= М2= М является наиболее интересным и он наиболее корректно рассматривается, поскольку при ![]() = 1 результат не зависит от критериев равенства давлений или сил. При этом поверхность “взаимодействия” потоков является плоскостью, перпендикулярной к r0 и делящей r0 пополам.
= 1 результат не зависит от критериев равенства давлений или сил. При этом поверхность “взаимодействия” потоков является плоскостью, перпендикулярной к r0 и делящей r0 пополам.
Правда, некоторое различие в числовом коэффициенте в законе взаимодействия может быть объяснено боковым перетеканием газов для плотных потоков и если учитывать для не очень плотных потоков глубину их взаимного проникновения. Оба эти фактора могут несколько уменьшить силу взаимодействия.
Рассмотрев корректно случай, когда M1= М2, легко обычными методами теории потенциала (считая, что имеет место суперпозиция потоков, что справедливо на больших расстояниях от тел) рассмотреть общий случай, когда M1> М2, считая, что M1= ![]() M2, где
M2, где ![]() >1. При этом естественно, окажется, что влияние тела M1 на М2 равно влиянию тела М2 на M1.
>1. При этом естественно, окажется, что влияние тела M1 на М2 равно влиянию тела М2 на M1.
Полагая, что
![]() (18)
(18)
найдём
![]() (19)
(19)
где мы приняли β1β2 = 18πG= const.
Мы пришли к закону взаимодействия между телами вида закона Ньютона или Кулона.
Если допустить, что количество газа, испускаемого телами за единицу времени, пропорционально массе тел, то надо положить
![]() (20)
(20)
где ![]()
Отсюда ![]() (21)
(21)
В общем случае можно написать,
![]() (22)
(22)
гдe θ= θ0(l-M22/4M12); при M2/M1=1 θ= 3θ0/4, при M2/M1→0 θ= 1. Фактор θ0<1 учитывает степень взаимного проникания потоков газов при их взаимодействии.
Рассмотрим теперь случай, когда тела, испускают не частички газа, а излучают кванты с массой покоя, равной нулю, причём будем считать, что для излучения справедливы те же уравнения состояния. Исключая из уравнений
![]() (23)
(23)
величину а найдём, что для излучения будет справедливо выражение
![]() (24)
(24)
где Е0 — полная энергия излучения.
Поскольку
![]() (25)
(25)
заменяя w через р, придём к уравнению
![]() (26)
(26)
На больших расстояниях от тел
![]() (27)
(27)
и для силы взаимодействия придём к прежнему результату.
Как было показано ранее (1), используемое решение имеет смысл при ∞> r≥ rmin= rкр, где ![]() Заменяя
Заменяя ![]() , найдём, что
, найдём, что ![]()
Естественно предположить, что rкp= R, где R — радиус излучающего тела. Тогда будем иметь
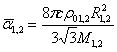 . (28)
. (28)
Решая совместно (22) и (28), найдём
![]() (29)
(29)
Таким образом, мы выразили величины ![]() и ρ01,2 через константу взаимодействия между телами, их массы и размеры.
и ρ01,2 через константу взаимодействия между телами, их массы и размеры.
В заключение выражаю благодарность И. Г. Арамановичу за ценные дискуссии.
Поступило
2 XII 1957
Дата установки: 31.12.2009
[вернуться к содержанию сайта]