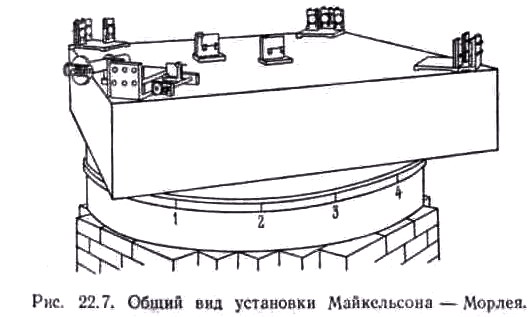
ФРАГМЕНТЫ ИЗ "ОПТИКИ" Г.С. ЛАНДСБЕРГА (М.: НАУКА, 1976)

Отрицательный результат опыта Майкельсона, не возбуждающий сомнения, имеет огромное принципиальное значение. Он является одним из наиболее надёжных опытов, подвергающих проверке вопрос об увлечении эфира движущимися телами и, следовательно, исходные положения теории Лоренца. Отрицательный результат его противоречит гипотезе неподвижного эфира и мог бы быть истолкован как доказательство полного увлечения эфира телами, т.е. вступил бы в кажущееся противоречие и с результатами опыта Физо. Было сделано поэтому немало попыток разрешить это противоречие.
Одна из них принадлежит Ритцу и состоит в допущении, что скорость света, испускаемого движущимся источником, слагается геометрически из скорости источника и скорости света от неподвижного источника, подобно скорости ядра, выстреливаемого быстро перемещающимся орудием (баллистическая
гипотеза). Нетрудно видеть, что если бы баллистическая гипотеза была справедлива, то опыт Майкельсона должен был бы дать отрицательный результат, ибо T1+T2 = 2T=2l/с. Однако астрофизические наблюдения над двойными звёздами решительно говорят против баллистической гипотезы. Действительно, представим себе двойную звезду (рис. 22.8) на расстоянии L от наблюдателя, одна из компонент которой S' имеет период обращения 2T и линейную скорость движения v. Если баллистическая гипотеза справедлива, то свет от компоненты S' в положении I дойдет до наблюдателя к моменту t1= L/(с– v), а в положении II – к моменту t2= T+ L/(с+ v), где Т – полупериод обращения.
Таким образом, наблюдаемое движение звезды может заметно отступать от законов Кеплера. В частности, при очень большом
L, возможно, что даже при v<<с получится t2<t1, т. е. видимое движение приобретает весьма прихотливый характер. Рассмотрение достаточного числа двойных звёзд показывает, что такое следствие баллистической гипотезы противоречит наблюдению и, следовательно, гипотеза Ритца должна быть оставлена.А. М. Бонч-Бруевич (1956 г.), применив для определения скорости света современные уточнённые методы, сравнил скорости света, идущего от правого и левого краёв Солнца, т. е. от источников, один из которых приближается, а другой отдаляется от нас со скоростью 2,3 км/с. Опыты с достаточной степенью точности показали, что различие в скорости света, предполагаемое по баллистической гипотезе, не имеет места.
Другое в высшей степени кардинальное допущение, предложенное для объяснения результатов опыта Майкельсона, было сделано, с одной стороны, Фицджеральдом, с другой – самим Лорентцом (1892 г.). Было высказано предположение, что в результате движения линейные размеры всех тел вдоль направления скорости сокращаются в отношении
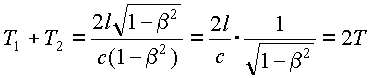 .
.
Линейчатые спектры, как уже упоминалось, представляют собой совокупность спектральных линий, составляющих известные системы, а не разбросанных в беспорядке по длинам волн. Установление связи между частотами отдельных линий впервые было сделано Бальмером (1885 г.).
Открытая им закономерность относится к четырем водородным линиям. Именно, оказалось, что длины волн, соответствующих этим линиям, можно выразить общей формулой
λ=
bm2/(m2–4),где
b=364,57 нм и т — ряд последовательных целых чисел 3, 4, 5, 6.Вводя вместо λ частоту
ν=c/λ, можно переписать формулу Бальмера в виде![]()
где
R — постоянная. В практической спектроскопии ν заменяют величиной N=ν/с=1/λ. Это так называемое волновое число показывает, сколько волн данной длины укладывается на протяжении 1 см. Таким образом, формула Бальмера приобретает вид![]()
где т= 3, 4, 5, 6. Величина
R связана с введённой выше постоянной b простым соотношением R=4/b.Во времена Бальмера были известны лишь 4 линии водорода, удовлетворяющие его формуле. В настоящее время известно около 30 линий Н в видимой части спектра, и частоты всех этих линий с поразительной точностью могут быть вычислены по формуле Бальмера, если придавать т целые значения 3, 4, 5... Постоянная
R, получившая название постоянной Ридберга, согласно современным данным равняется 1,097677587·105 см–1. Число знаков, с которыми определена постоянная Ридберга, с одной стороны, показывает, какой степени точности достигла современная спектроскопия, а с другой — иллюстрирует, насколько формула Бальмера удачно передаёт результаты наблюдений. Ещё убедительнее демонстрирует точность формулы Бальмера табл. 38.1, сопоставляющая измеренные значения длин волн бальмеровской серии в спектре водорода и значения, вычисленные по формуле Бальмера.Таблица 38.
1|
т |
λ (выч.), им |
λ (набл.), нм |
m |
λ (выч.), нм |
λ (набл.), нм |
|
3 |
656,280 |
656,280 |
18 |
369,159 |
369,156 |
|
4 |
486,138 |
486,133 |
19 |
368,686 |
368,683 |
|
5 |
434,051 |
434,047 |
20 |
368,284 |
368,281 |
|
6 |
410,178 |
410,174 |
21 |
367,938 |
367,936 |
|
7 |
397,011 |
397,007 |
22 |
367,639 |
367,636 |
|
8 |
388,909 |
388,905 |
23 |
367,380 |
367,376 |
|
9 |
383,543 |
383,539 |
24 |
367,151 |
367,148 |
|
10 |
379,793 |
379,790 |
25 |
366,950 |
366,947 |
|
11 |
377,067 |
377,063 |
26 |
366,772 |
366,768 |
|
12 |
375,018 |
375,015 |
27 |
366,613 |
366,610 |
|
13 |
373,440 |
373,437 |
28 |
366,441 |
366,468 |
|
14 |
372,197 |
372,194 |
29 |
366,344 |
366,341 |
|
15 |
371,201 |
371,197 |
30 |
366,229 |
366,226 |
|
16 |
370,389 |
370,386 |
31 |
366,125 |
366,122 |
|
17 |
369,719 |
369,715 |
Эта таблица ясно показывает, что мы имеем дело не просто с удачно подобранной эмпирической формулой, а с выражением какой-то внутриатомной закономерности. Это убеждение ещё более укрепилось, когда обнаружилось, что открытые позже линии водорода, лежащие в
ультрафиолетовой и инфракрасной частях спектра, также укладываются в аналогичные формулы, а именно:серия Лаймана (в далёкой ультрафиолетовой области) — в формулу
N=R(1/12–1/m2) (m=2, 3, 4); (205.2)
серия Пашена (в близкой инфракрасной области) — в формулу
N=R(1/32–1/m2) (m=4, 5, 6, 7, 8); (205.3)
серия Брэккета (в более отдалённой инфракрасной области) — в формулу
N=R(1/42–1/m2) (m=5, 6); (205.4)
серия Пфунда (ещё дальше в инфракрасной области) — в формулу
N=R(1/52–1/m2) (т =6, 7).
Все линии водородного спектра можно, следовательно, разделить на ряд серий, объединяемых общей формулой:
N=R(1/n2–1/m2), (205.5)
где п=
1, 2, 3, 4, 5, т — целые числа, причём т>п, a R — одна и та же постоянная, упоминавшаяся выше. Число п определяет серию, т — отдельную линию этой серии; при п=1 получаем cepию Лаймана, при п=2 — серию Бальмера, при n=3 — серию Пашена, при п=4 — серию Брэккета, при п=5 — серию Пфунда. На рис. 38.1 схематически изображен полный спектр водорода и отдельные серии, на которые его можно разложить. Каждая серия состоит из ряда линий, расстояния между которыми, как и следует из формулы, уменьшаются в сторону коротких длин волн.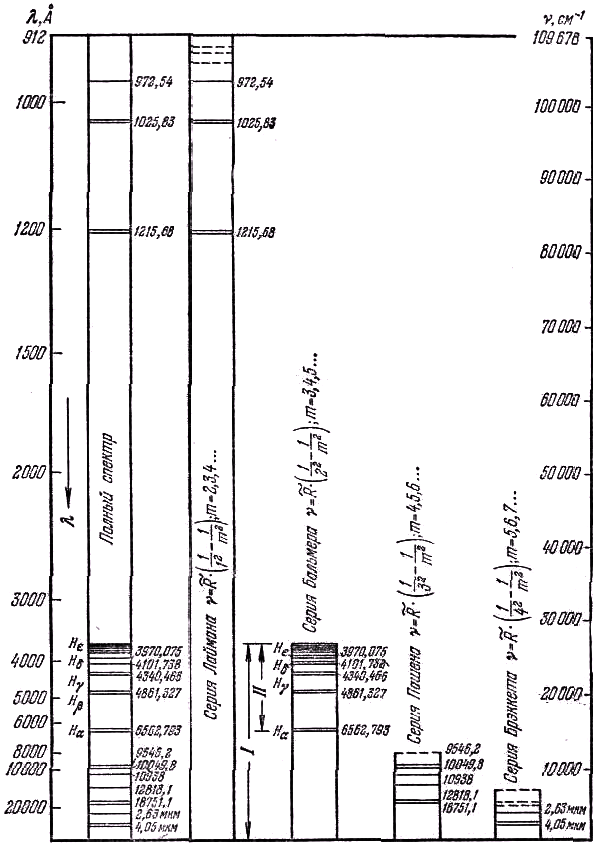
Рис. 38.1. Схематическое изображение спектра атома водорода: полный спектр и отдельные спектральные серии.
Постепенно увеличиваясь, частоты линий стремятся к определённому пределу, величину которого легко найти из сериальной формулы
. Иногда наблюдается слабый сплошной спектр, примыкающий к границе серии со стороны больших частот. На рис. 38.2 приведена фoтoгpафия линий серии Бальмера.
Рис. 38.2. Фотография линии серии Бальмера.
Успех Бальмера направил внимание исследователей на поиски сериальных зависимостей в спектрах других веществ. В первую очередь были исследованы спектры щелочных металлов, затем щелочноземельных и некоторых других элементов. Несмотря на трудность расшифровки, и здесь найдены были серии, и, что очень важно, полученные формулы очень
напоминали сериальную формулу для водорода. Отличие сводится к поправочным членам α и β, имеющим для водорода значения, равные нулю:N=R[1/(n+α)2–1/(m+β)2]. (205.6)
Каждому элементу соответствует несколько таких поправочных членов, с помощью которых можно выразить все характерные для данного элемента серии. Так, например, для натрия эти поправки имеют значения –1,35, –0,87, –0,01 и 0, так что все четыре известные серии натрия выражаются в виде
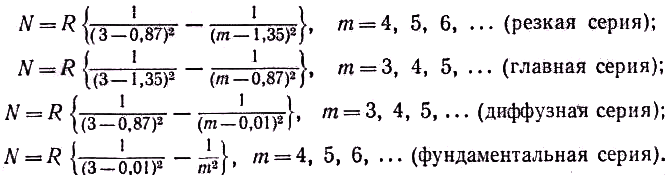
Как мы видим,
n во всех сериях равно 3, а т принимает целые значения ≥3. Поправочные члены входят в различных, хотя и не во всех мыслимых комбинациях (правила отбора). R имеет почти то же значение, что и в серии Бальмера.Более тщательные измерения показывают, что
R слегка увеличивается по мере возрастания атомного веса, имея для водорода значение 109678 см–1, а для наиболее тяжёлых атомов — 109737 см–1, причём, начиная примерно с хлора, нарастание R практически уже незаметно. В частности, для натрия RNa= 109735 см–1.Спектры щелочных и щелочноземельных металлов и других элементов гораздо сложнее спектра водорода. Одним из отличий, имеющих место и в других сложных элементах, является мультиплетный характер линий: линии состоят из нескольких (две, три и более) компонент с близкими значениями частот. Частоты отдельных компонент также подчинены определённым закономерностям. Разыскивать закономерности в таких сложных спектрах нелегко, и это явилось в значительной степени делом догадки и остроумия. Благодаря работам Ридберга и других выяснились некоторые правила, помогающие обнаруживать и выделять отдельные серии. В настоящее время теория атома позволила обосновать многие такие правила. В частности, принадлежность линии к той или другой серии можно установить по характеру аномального расщепления в магнитном поле (см. § 172).
Исследования Ридберга (1890 г.) выяснили универсальность постоянной
R и возможность представления отдельных частот двучленными формулами приведённого выше типа, т. е. в виде разности двух членов (термов). Кроме того, оказалось, что различные термы (зависящие от α и β) могут комбинироваться попарно, давая начало новым сериям (комбинационный принцип Ритца, 1908 г.). Таким образом выясняется, что физический смысл имеет именно терм. Особенности атома проявляются в поправочных членах сериальных формул и в мультиплетности линий (точнее, термов).Установление сериальных закономерностей, связь между сериями (принцип Ритца), универсальность постоянной Ридберга — всё свидетельствовало о глубоком физическом смысле открытых законов. Тем не менее, попытки установить на основании этих законов внутренний атомный механизм, обусловливающий найденные закономерности, потерпели решительную неудачу. Было ясно, что каждая серия полностью вызвана одним и тем же механизмом. Между тем трудно представить себе возможность излучения целого ряда частот таким простым атомом, как, например, атом водорода. Известны, конечно, типы механических излучателей, дающих ряд колебаний, например струна. Однако спектр такого излучателя состоит из
основной частоты и её обертонов, представляющих целые кратные от основной, даже отдалённо не напоминая закономерностей, наблюдаемых в спектральных сериях.. Были попытки придумать такие типы излучателей, которые давали бы частоты, связанные формулами, аналогичными формулам спектральных серий (Ритц, закреплённые мембраны). Но попытки эти кончились неудачей. Ритц показал, что классическими законами колебательных систем нельзя объяснить законы спектральных серий.И действительно, решение задачи было найдено в 1913 г. Бором путём привлечения для объяснения атомных закономерностей теории квантов; таким образом, оказалось, что классические законы, установленные в макроскопических явлениях, недостаточны для объяснения строения атомов.
[вернуться к содержанию сайта]
Дата установки: 28.10.2006
Последнее обновление: 16.02.2009