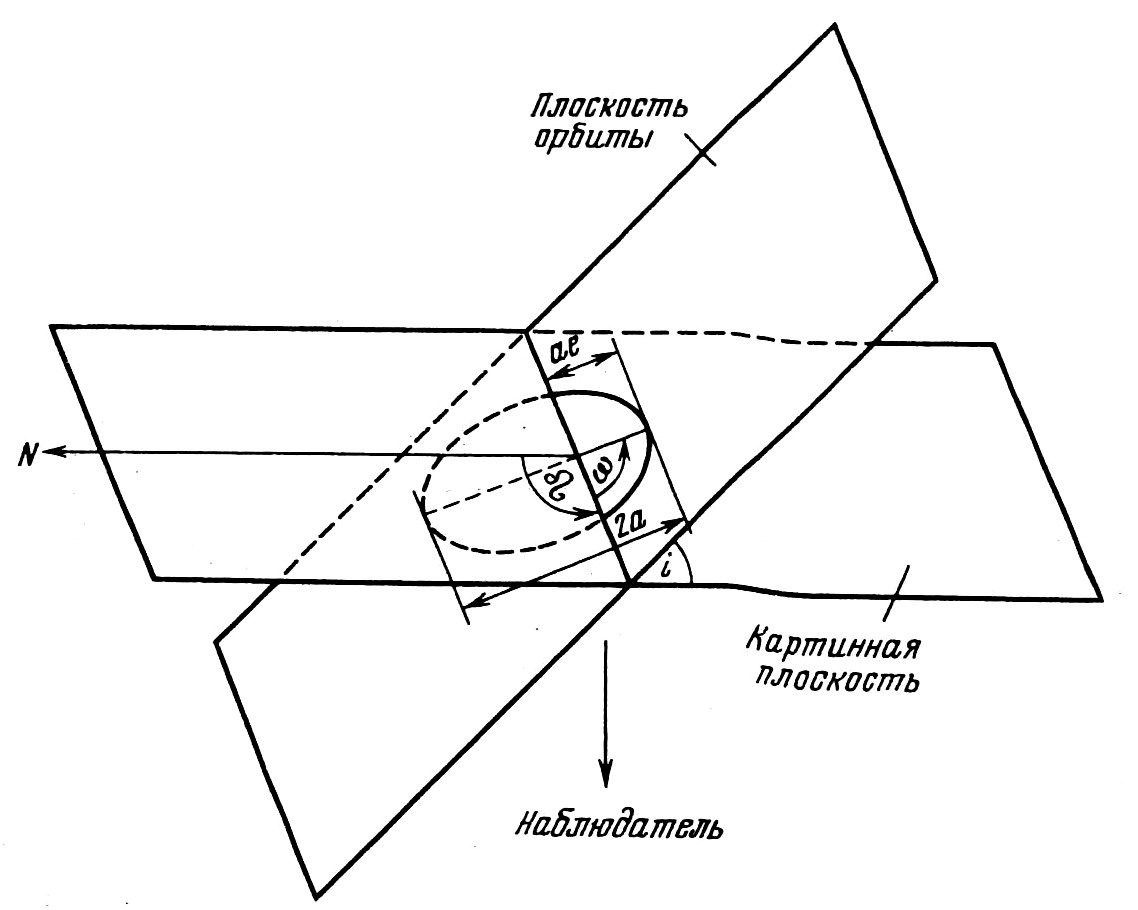
Рис. 1.3. Орбитальная плоскость, картинная плоскость и элементы орбиты.
[вернуться к содержанию сайта]
Термин элементы орбиты возник при изучении движения планет. Чтобы определить движение планеты по орбите, необходимо знать шесть величин; обычно выбираются следующие элементы (рис. 1.3):
1. Два угла i, Ω, которые определяют положение плоскости орбиты в пространстве по отношению к плоскости отсчёта. Выбор последней произволен: для орбит планет это может быть плоскость земной орбиты или же неизменная плоскость Солнечной системы.

Рис. 1.3. Орбитальная плоскость, картинная плоскость и элементы орбиты.
2. Третий угол ω, определяющий ориентацию большой оси эллиптической орбиты в плоскости орбиты. Во многих исследованиях динамики Солнечной системы удобнее использовать другой угол, ώ, равный ω+Ω. Этот суммарный угол называется долготой перигелия; обратите внимание, что он составлен из двух углов, лежащих в различных плоскостях.
3. Две величины a (большая полуось) и e (эксцентриситет), которые определяют размеры и форму эллипса.
4. Момент T, соответствующий данному положению планеты на орбите (обычно время прохождения через перигелий). Период P не является необходимым самостоятельным элементом, так как в пределах Солнечной системы все периоды даются третьим законом Кеплера:
a3/P2=const
Орбиту двойной системы можно определить аналогичным образом, хотя выбирается другая плоскость отсчёта, а период связан с большой полуосью законом Кеплера, выраженным в обобщённом виде:
a3/P2~m1+m2,
где m1 и m2 – массы обеих звёзд. Для полного динамического описания системы требуется, следовательно, знать период P, и его можно рассматривать в качестве дополнительного элемента орбиты. Для определения орбиты двойной используются следующие величины:
P – орбитальный период, обычно выраженный в сутках (у спектральной или затменной двойной) или в годах (у визуально-двойной);
i – наклонение плоскости орбиты к картинной плоскости;
Ω – п
озиционный угол (измеряемый от направления на север через восток) линии узлов, соединяющей точки пересечения орбитальной и картинной плоскостей; измеряется в картинной плоскости;ω – у
гол между направлением на восходящий узел (в котором звезда пересекает картинную плоскость, удаляясь от наблюдателя) и направлением на точку наибольшего сближения обеих звёзд (периастр). Этот угол измеряется в плоскости орбиты в направлении орбитального движения. Наблюдатели визуально-двойных всегда дают значение ω, соответствующее более слабой компоненте системы, тогда как наблюдатели спектрально-двойных и затменных систем обычно приводят величину ω для орбиты главной компоненты. В любой системе эти значения отличаются на 180°. Угол ω называется обычно долготой периастра. Термин выбран не очень удачно, поскольку вызывает аналогию с долготой перигелия, которая измеряется в двух различных плоскостях, тогда как долгота периастра измеряется только в одной плоскости. Мы обращаем внимание на это различие, поскольку в некоторых опубликованных исследованиях по динамике орбит двойных систем были спутаны углы ω и ώ;a – большая полуось орбиты, обычно выражаемая в километрах или астрономических единицах;
e – эксцентриситет орбиты, безразмерная величина от нуля до единицы;
T – момент времени, в который обе звезды проходят через периастр.
Величины P, i, ω, e и T можно определить из наблюдений визуально-двойной. Однако восходящий и нисходящий узлы орбиты невозможно различить без учёта данных о лучевых скоростях звёзд. Использование только визуальных наблюдений может привести к ошибке в 180° при определении значения Ω. Условились считать, что 0°≤i≤90°, если видимое движение прямое, и 90°≤i≤180° в противоположном случае; узел, для которого Ω<180°, считают восходящим, если нет доказательств противоположного. Видимую большую полуось a (измеряется в секундах дуги) можно найти из визуальных наблюдений, но при отсутствии независимого определения расстояния измеренное значение нельзя преобразовать в абсолютную величину a. Если проведены наблюдения лучевых скоростей, то их можно использовать, чтобы задать характерный размер орбиты и таким образом определить расстояние. По третьему закону Кеплера можно оценить большую ось и, следовательно, расстояние, если принять, что массы компонент являются нормальными для их спектральных классов. Такая оценка расстояния, выраженная через параллакс, обычно называется динамическим параллаксом.
Какова надёжность впервые полученных орбитальных элементов? В предыдущем разделе показано, что погрешность при вычислении одного орбитального элемента неминуемо повлечёт за собой ошибки в вычислениях других элементов. Точность, достигаемая при одновременном определении слишком многих неизвестных, бывает иногда иллюзорной. Почти круговую орбиту можно обрабатывать как круговую, хотя введение двух дополнительных параметров е и ω почти всегда улучшает согласие с наблюдениями. Хорошим критерием надёжности орбитальных элементов является их воспроизводимость. Совершенно независимые определения орбитальных элементов в различные эпохи были выполнены для крайне малого числа систем. Например, больше чем одну эпоху наблюдалось лишь около четверти спектрально-двойных. Около половины из этого числа имеют значительные или подозреваемые изменения "орбитальных элементов" [39], большая часть которых носит характер, не соответствующий реальным изменениям в двойной системе. Периодические колебания V0 можно приписать присутствию третьего тела, а систематическое изменение значения ω обычно относят на счёт внутреннего строения компонент, хотя оно может быть вызвано присутствием третьего тела и, конечно, релятивистскими эффектами. Не так легко объяснить сильные, неправильные колебания К и е. Поскольку эксцентриситет часто определён плохо, естественно сконцентрировать внимание на элементе К, в котором обычно находят эти изменения. Для некоторых систем (например, AR Кассиопеи и δ Козерога) вариации К могли бы означать на первый взгляд флуктуации общей массы системы. Многие наблюдения, относящиеся к первой эпохе, были получены при низкой дисперсии, что, без сомнения, увеличивает измерительные и фотографические ошибки, которые могут систематически искажать величину К (гл. 5), особенно для спектрально-двойных, у которых видны спектры обеих компонент. Однако у двух упомянутых систем виден спектр только одной компоненты. Если метод решения не подходит, то можно получить ошибочные элементы, определённые для двух различных эпох. Такая ситуация весьма вероятна, когда наблюдения распределены неравномерно по кривой лучевой скорости. На определении орбитальных элементов могут сказаться пульсации одной из компонент или присутствие необнаружимого третьего тела. Значения элементов ω и e, найденные из спектроскопических наблюдений, могут сильно отличаться от вычисленных из кривой блеска. Не приходится сомневаться, что источником ошибок является кривая лучевых скоростей. Струве считал этот факт доказательством того, что во многих системах звёздные спектры искажены спектрами газовых потоков (гл. 8). На рис. 1.4 показано распределение значений ω [47]. Оно очень далеко от равномерного распределения, ожидаемого при случайной ориентации орбиты в пространстве, и, следовательно, многие значения ω сомнительны.
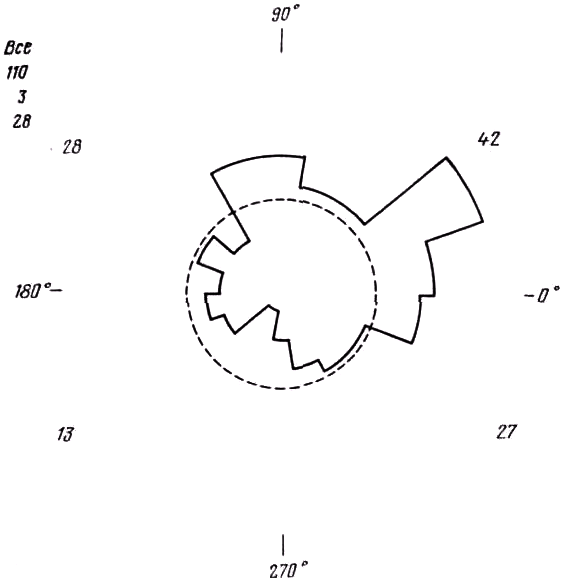
Рис. 1.4. Распределение ω для всех систем, у которых определён орбитальный эксцентриситет из "Шестого каталога орбитальных элементов спектрально-двойных систем".
Числа в каждом углу обозначают общее число систем в каждом квадранте. Вверху слева приведены: общее число, среднее в интервале 10° (штриховал линия) и среднее в интервале 90°.
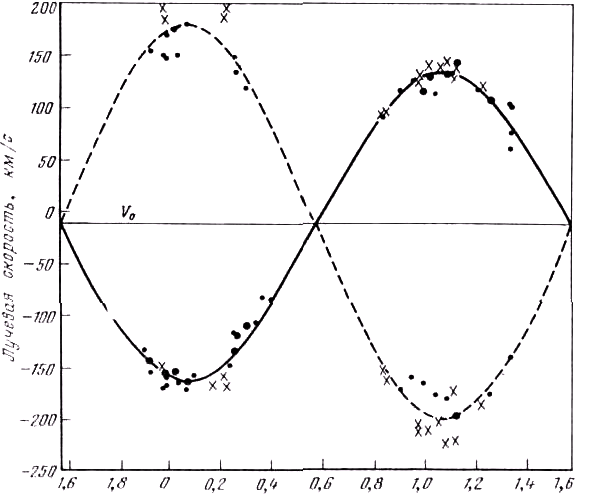
Дни
Рис. 1.5. Кривая лучевых скоростей для спектрально-двойной с двумя спектрами HD 175544 [469].
Из всей этой информации следует, что осмотрительнее рассматривать орбитальные элементы спектрально-двойных скорее как параметры, более или менее хорошо описывающие наблюдаемое изменение скорости в данный период, нежели меру физических свойств данной двойной системы. Уверенность в истинности элементов системы можно обрести только после получения одних и тех же значений по двум или трём независимым рядам наблюдений. Желательно определить элементы для гораздо большего числа систем и для более чем одной эпохи.
Имеются серьёзные свидетельства изменения кривых блеска от одной эпохи к другой (гл. 8). Эти изменения могут поставить под сомнение любое определение элементов орбиты из наблюдений затменной двойной в течение одной лишь эпохи. Высокая точность, на которую иногда претендуют подобные элементы, не вызывает доверия. Кроме того, некоторые кривые блеска фактически неопределимы в принципе, например, у систем с неглубокими частными затмениями или у систем, одна из компонент которых является неправильной переменной. Из одних и тех же наблюдений для таких систем можно получить широкий разброс данных о потемнении к краю диска и отношении радиусов.
Казалось бы, что визуально-двойные не вызывают подобных трудностей, так как звёзды можно разрешить, а их относительное положение измерить. Тем не менее при определении элементов возникают затруднения часто потому, что элементы вычисляются по очень малой дуге орбиты [481]. Порой звёзды имеют почти одинаковый блеск и по временам становятся неразрешимыми. Когда звёзды вновь становятся разрешимыми, наблюдатель, возможно, окажется не в состоянии отличить, которая из них является главной компонентой, а которая – спутником. Таким образом, можно получить по крайней мере два набора элементов, причём даже периоды не будут совпадать, хотя каждый из них одинаково хорошо удовлетворяет наблюдениям. В подобных случаях единственным способом установления истины являются наблюдения лучевой скорости (рис. 1.5). Поэтому для всех типов двойных следует с осторожностью относиться к элементам, определённым из одной серии наблюдений.
Струве и Хуанг [456] предположили, что различные типы переменных звёзд можно расположить в непрерывную последовательность, на одном конце которой будут правильные спокойные переменные – цефеиды, а на другом – новые звёзды. В предыдущем разделе было показано, что многие (а возможно, все) новые принадлежат к двойным системам, обычно короткопериодическим. Струве и Хуанг предположили, что цефеиды являются либо одиночными, либо компонентами очень широких пар. Абт [3] нашёл, что только 2% цефеид являются членами двойных систем, и подчеркнул, что вряд ли цефеиды принадлежат к системам с периодами меньше 100 сут, потому что в такой системе эволюционирующие звёзды классов О или В достигали бы предельной поверхности Роша, определяемой влиянием спутника, раньше, чем успевали бы достаточно расшириться, чтобы превратиться в цефеиды.
Впоследствии исследование цефеид провёл Т. Эванс [116]. Он нашёл, что в выборке из 40 цефеид I типа 15% обладают некоторыми признаками принадлежности к двойным системам. Цефеиды – это гиганты и сверхгиганты; процент двойных среди гигантов, найденный Яшеком и Яшек, не слишком отличается от приведённого значения, хотя в более поздней работе Яшека и Гомеца он заметно ниже. Тем не менее открыть двойные среди переменных звёзд очень трудно, поскольку внутренние изменения в самой звезде искажают и даже скрадывают вариации блеска и скорости, ожидаемые от тесной двойной. Многие истинные переменные являются звёздами высокой светимости, наблюдаемыми с больших расстояний, поэтому открытие визуальных компонент затруднено. Например, до сих пор нет единого мнения относительно того, связан ли физически визуальный спутник δ Цефея с этой переменной [118, 528]. Поэтому не исключено, что истинная частота двойных среди Цефеид выше наблюдаемой, и нет убедительных свидетельств того, что она отличается от частоты, найденной для всего класса звёзд-гигантов в целом. Однако Эванс нашёл, что все известные орбитальные периоды значительно больше 100 сут. Имеются данные, что систем с периодами около года меньше, чем с длинными периодами. Малый объём выборки позволяет сделать только предварительное заключение. Эванс также установил, что у цефеид в двойных наблюдается тенденция к изменениям блеска с меньшими амплитудами, нежели у одиночных.
Более сложные собственные изменения обнаружены у звёзд типа β Цефея. В некоторых фазах их спектры показывают двойные линии, поэтому возникла гипотеза, что многие из них являются двойными, хотя теперь известно, что удвоение линий вызвано другими причинами. В изменениях блеска у них обычно выделяются два периода и порождённый их наличием период биений. Ван Хооф [488] предположил, что у некоторых из этих звёзд можно найти ещё более сложную периодичность. Он считает, что многие из них принадлежат к двойным системам. Симон и Стотерс [428] предположили, что все звёзды типа β Цефея являются членами тесных двойных, в которых имеет место обмен массами между компонентами. Внешние слои переменной ныне компоненты содержат вещество, богатое гелием, отторгнутое от первоначально более массивной звезды. Таким образом, средняя молекулярная масса этих слоёв выше, чем у звезды в целом, и предполагается, что этим различием и обусловлены пульсации звезды. Наблюдательные свидетельства в пользу предположения, что все звёзды типа β Цефея – члены тесных двойных систем, сомнительны. Две звезды этого типа: 16 Ящерицы и σ Скорпиона – приведены в "Шестом каталоге" [38], хотя орбиты обеих определены ненадёжно. Очень трудно отделить вариации лучевой скорости, связанные с орбитальным движением, от вариаций, вызванных собственными изменениями, и, возможно, до сих пор нет полной уверенности в том, что эти звёзды являются двойными. С другой стороны, известная двойная α Девы показывает как кривую блеска типа β Цефея, так и эллипсоидальные изменения [426], Фитч опубликовал* орбитальные элементы для самой β Цефея, и ван Хооф представил аргументы в пользу того, что θ Змееносца является двойной [489]. Тем не менее ещё не известен процент двойных среди этих переменных. Снова обнаруживается, что спутники, если они существуют, влияют на физические изменения блеска. Ван Хооф считает, что орбитальный период σ Скорпиона очень близок к точному кратному периода биения. Фитч пытался объяснить периодические модуляции этого типа изменений влиянием приливов, вызываемых спутником у переменной звезды. Некоторые двойные системы были найдены в родственном классе переменных типа δ Щита.
Данных для общего рассмотрения частоты двойных в других классах переменных звёзд недостаточно. Известно, что несколько физических переменных звёзд принадлежит к двойным системам. Например, долгопериодическая переменная Х Змееносца является членом ADS 11524 [117].
––––––––––––––––––––––
* Fitch W.S., Astrophys. J., 158, 269-280 (1969). - Прим.ред.
Рассмотрение в предыдущей главе систем, имеющих компоненту, окружённую протяжённой атмосферой, естественным образом привело к рассмотрению потоков или облаков газа в пространстве между двумя компонентами. Многие виды двойных систем показывают признаки присутствия в них газовых потоков или облаков и настоящая глава посвящена суммированию этих данных. Вещество, находящееся между компонентами двойной, обычно называют околозвёздным. Трудно провести чёткую грань между околозвёздным веществом и протяженными атмосферами, хотя в некоторых системах происходят явления, которые совершенно невозможно приписать какому-либо типу атмосферы. В качестве полезного рабочего определения можно называть околозвёздным вещество, находящееся по соседству с двойной системой и выброшенное одной из компонент, но временно или постоянно принадлежащее не отдельной компоненте, а системе в целом.
Существование околозвёздного вещества в системе может обнаруживаться разными путями. У многих систем по крайней мере одна компонента заполняет свою полость Роша; вследствие этого имеются основания для предположения, что звезда неустойчива. В таких системах можно ожидать присутствия околозвёздного вещества. Изменения периода, обнаруживаемые у многих систем, рассмотрены в гл. 4, где показано, что такие изменения могут указывать либо на потерю массы всей системой, либо на обмен массой между компонентами. Каждая из этих возможностей подразумевает существование околозвёздного вещества. Список систем, показывающих изменения периода, был составлен Вудом и Форбсом [520], хотя многие из перечисленных ими "изменений" находятся на пределе обнаружения. Однако существование околозвёздного вещества следует не только из этих наблюдений; его можно непосредственно наблюдать, если оно оказывает влияние на спектр систем, добавляя к общему спектру дополнительные линии поглощения или излучения. Излучение можно наблюдать непосредственно. Дополнительные линии поглощения можно заметить, если подвергнуть спектр тщательным спектрофотометрическим измерениям. Однако их можно обнаружить по измерениям лучевых скоростей, так как околозвёздные составляющие линий поглощения могут исказить весь профиль линии и внести ошибку в измеряемую скорость. Поэтому деформация кривой лучевых скоростей является свидетельством существования околозвёздного вещества. Если система является затменной двойной, то деформацию кривой лучевых скоростей можно распознать по различию элементов е и ω, найденных из кривой блеска и из кривой лучевых скоростей. Этот эффект, уже упомянутый в гл. 1, называется эффектом Барра. Деформацию кривой лучевых скоростей можно также выявить, если два ряда наблюдений, выполненных в различные эпохи, дают разные орбитальные элементы; по крайней мере одна из кривых должна быть деформированной. Этот эффект обнаруживается, если линии различных атомов или ионов в спектре звезды дают разные кривые лучевых скоростей. Все эти явления служат свидетельством существования околозвёздного вещества. Эти критерии были общепризнанны почти сразу после пионерских исследований околозвёздного вещества, предпринятых Струве. Кривые блеска многих систем также выдают существование околозвёздного вещества. Этот путь был принят менее охотно: если для воздействия в узких пределах длин волн спектральной линии необходимы сравнительно малые количества вещества, то многие сомневались в том, хватит ли вещества в системе, чтобы произвести обнаружимый эффект в пределах широких полос U, В, V при фотометрии. Тем не менее Ханзен [155] нашёл, что электронное рассеяние в газовом потоке достаточно, чтобы произвести в кривой блеска RZ Щита изменения, сравнимые с наблюдённым эффектом; подобные вычисления проделал Гюнтер [149] для системы SX Кассиопеи (гл. 9).
Имеющиеся данные относительно существования околозвёздного вещества суммированы дальше в этой главе в трёх разделах: деформация кривых лучевых скоростей; спектрофотометрические данные, включая существование линий излучения; деформация кривых блеска. В пределах каждого раздела приводятся данные для систем типа Алголя (т.е. систем, имеющих в качестве главной компоненты звезду главной последовательности позднего В или раннего A спектрального класса, а в качестве спутника – субгигант позднего класса); систем, содержащих массивные звёзды раннего класса (например, β Лиры); систем типа W Большой Медведицы; катаклизмических переменных. Вместе с системами типа Алголя рассмотрены три системы: SX и RX Кассиопеи и UX Единорога. Обе компоненты этих систем принадлежат к гигантам, хотя, возможно, ни одна не заполняет свою полость Роша. Свидетельства существования околозвёздного вещества в этих системах подобны найденным для систем типа Алголя, хотя подобие здесь может оказаться чисто внешним. Данные о том, что системы, содержащие звёзды с протяжённой атмосферой, включают также околозвёздное вещество, уже представлялись в гл. 7.
Системы типа Алголя. Хотя деформация кривой лучевых скоростей самого Алголя невелика, именно среди систем, которые теперь носят название систем типа Алголя, она была обнаружена впервые. Наиболее известный пример – U Цефея (рис. 8.1). Хотя вторичный минимум кривой блеска этой системы неглубок и иногда бывает деформирован, он достаточно ясно показывает, что е cos ω близко к нулю. Обычно предполагается, хотя и не всегда строго соблюдается, что само е также близко к нулю. Однако кривые лучевых скоростей совершенно разных эпох дают значения е cos ω, изменяющиеся от 0,21 до 0,45, откуда следует, что е близко к 0,2. Этот род деформаций характерен для систем типа Алголя, а также для систем, подобных SX Кассиопеи. Возможно, экстремальным случаем является система S Малого Коня [364, 366], изменения скорости у которой почти полностью замаскированы на протяжении всего периода, кроме последнего момента перед главным затмением. Кривая лучевых скоростей DN Ориона несколько деформирована [434], а так как орбитальное изменение скорости для этой системы мало, деформация, возможно, играет важную роль. Кривая U Стрелы, подобно кривой самого Алголя, показывает лишь небольшой спектроскопический эксцентриситет, но на кривой лучевых скоростей RW Тельца деформация выражена сильнее. Крайних пределов эффект достигает на кривой лучевых скоростей RZ Щита, которая имеет ступенчатый вид (рис. 8.2). Кривая U Цефея выглядит аналогично, но "ступени" менее выражены. Подобные кривые лучевых скоростей, безусловно, не могут являться следствием кеплеровского движения. Ханзен и Мак-Намара предполагают, что скачки в наклоне кривой возникают при тех фазах, когда некоторая часть газового потока, по-видимому существующего в системе, появляется или исчезает позади одной из звёзд. Асимметрия профилей линий гелия в спектре особенно заметна в этих фазах. Ступенчатые кривые лучевых скоростей внешне напоминают кривые звёзд типа β Цефея. Обычно считается, что изменение лучевых скоростей последних вызывают ударные волны в их атмосферах. Существование ударных воли в околозвёздном веществе рассматривалось Бирманом [51], Кржижем [253] и Горбацким [142]. В частности, Бирман находит, что при столкновении потока вещества с одной из компонент неминуемо должна образоваться ударная волна. Возможно, что её влияние мы наблюдаем у RZ Щита.
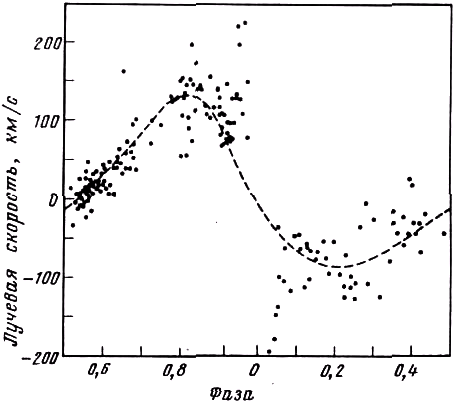
Рис. 8.1. Кривая лучевых скоростей U Цефея по наблюдениям в Виктории в 1963 - 1968 гг.
Штриховая линия проведена от руки, чтобы показать общую тенденцию скоростей. Кривая явно не имеет синусоидальной формы, которую следует ожидать для круговой орбиты.
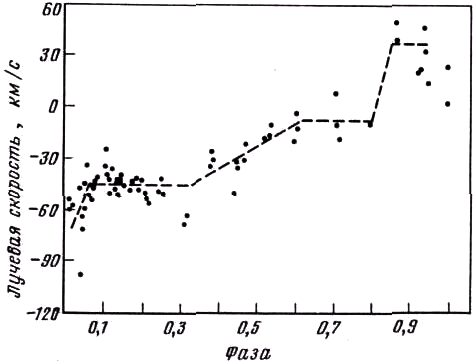
Рис. 8.2. Кривая лучевых скоростей RZ Щита, полученная по всем линиям водорода, кроме Нα.
Штриховая линия подчёркивает ступенчатый вид кривой. По данным Хансена и Мак-Намары [156].
Струве считал, что эти деформации кривых лучевых скоростей наблюдаются вследствие искажения профилей линий в спектрах этих систем при некоторых фазах. Гарди [158] ввёл систематические поправки в измерения скоростей U Цефея, произведённые Струве, и получил правдоподобную круговую орбиту. К сожалению, тот же приём введения поправок, применённый к последующим наблюдениям, не дал возможности получить те же самые значения для орбитальных элементов. Струве утверждал, что деформация профилей линий в свою очередь вызывается комбинацией спектра газового потока, летящего от спутника к главной компоненте, со спектром последней. Он обычно предполагал, что поток виден в проекции на диск более яркой звезды, и, следовательно, его спектр является спектром поглощения, дополнительным к линиям поглощения в спектре звезды. Таким образом, в его интерпретации деформированный профиль линии всегда содержит широкую линию поглощения от спектра звезды и узкую линию от спектра потока. Однако не исключено, что при некоторых фазах поток виден в излучении. Так, при фазе 0,75P, измеряемой от главного затмения, можно увидеть некоторую часть потока между двумя звёздами в проекции на фон неба. Результирующее излучение, возможно, не будет обнаружено в виде линии излучения, а будет частично заполнять профиль линий поглощения. Этот профиль также выглядел бы асимметричным (рис. 8.3), но метод разделения линий потока и звезды отличался бы от применённого Гарди.
Приведённые примеры деформации кривых лучевых скоростей представляют собой хорошие частные примеры эффекта Барра. Барр [29] открыл, что у большинства систем преобладают значения ω между 0 и 180°, а не между 180 и 360°. Хотя на результаты Барра повлияло включение в его выборку некоторого числа цефеид, последующие исследования подтвердили этот результат. Избыток в значениях ω для систем типа Алголя сильнее всего заметен в первом квадранте (рис. 8.4). Возможная связь этого избытка с деформацией кривой лучевых скоростей показана в работе Саведова [412], который сравнивал значения e cos ω, полученные из кривых блеска и кривых лучевых скоростей для нескольких затменных систем. Кривые блеска указывают на почти круговые орбиты, тогда как кривые лучевых скоростей дают высокие значения e cos ω. Таким образом, имеются важные статистические свидетельства, подтверждающие результаты, полученные для систем типа U Цефея.
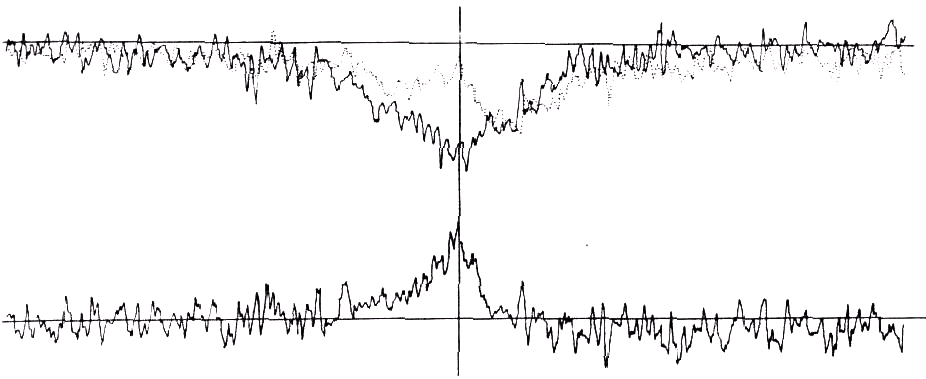
Рис. 8.3. Микрофотометрическая запись профиля линии Нα в спектре U Цефея при фазе 0,79P (от главного затмения), наложенная на подобную же запись при фазе 0,52P (сплошная кривая).
Линия выглядит двойной при 0,79 P но эта диаграмма показывает, что её профиль лежит полностью внутри профиля для 0,52P. Нижняя запись показывает эмиссию, которая должна присутствовать при 0,79P, если различие профилей вызывается эмиссией от потока между звёздами. Длинноволновый конец спектра находится справа.
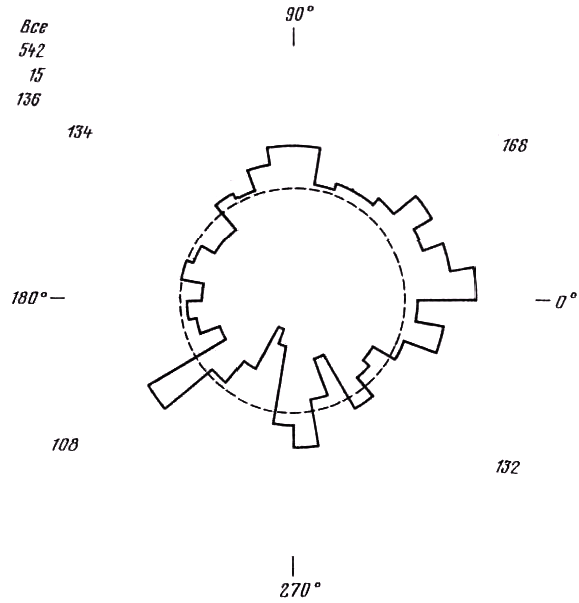
Рис. 8.4. Эффект Барра для затменных систем с эксцентрическими (спектроскопическими) орбитами.
Вследствие влияния селекции эта группа, возможно, содержит высокий процент систем типа Алголя. Представление результатов аналогично рис. 1.4.
Кривые лучевых скоростей U Цефея, полученные в разные эпохи, не всегда согласуются, подтверждая этим гипотезу о деформации кривых, тогда как системы типа Алголя дают мало примеров расхождения этих кривых, полученных по различным линиям спектра главной звезды. Это объясняется тем, что спектр главной компоненты принадлежит обычно к позднему классу В или раннему А, а сама звезда часто вращается очень быстро, и можно увидеть и измерить только линии водорода. Тем не менее Струве [452] и Мак-Намара [301] нашли различие между кривыми лучевых скоростей, построенными по линиям водорода, с одной стороны, и металлов – с другой, в спектре U Стрелы. Спутник является, в сущности, тёмным, так что это расхождение ни коим образом нельзя приписать "отражению" света спутника от главной звезды. Его скорее следует рассматривать в качестве дополнительного доказательства того, что при некоторых фазах искажается но крайней мере профиль линии водорода. Линия К Ca II в спектрах этих систем часто имеет меньшую амплитуду изменения лучевых скоростей, нежели линии водорода, как считают, в результате слияния линий межзвёздной компоненты с линиями звезды. Такое объяснение представляется неправдоподобным для поздних звёзд спектрального класса U потому, что эти звёзды, по крайней мере в хорошо изученных тесных двойных, редко находятся на достаточно большом расстоянии, чтобы могли образоваться сильные межзвёздные линии. Например, U Цефея находится от нас на расстоянии 400 пс на галактической широте 17°. В её спектре нет и следа межзвёздной линии D натрия, но центральная составляющая линии К Ca II (линия имеет очень сложную структуру) колеблется в фазе с орбитальным движением с полной амплитудой в пределах от 25 до 30 км/с (возможно, составляющей одну шестую от общей амплитуды скорости линий водорода); правда, это значение не вполне достоверно, так как истинная кривая лучевых скоростей системы не была выделена. Также имеет место небольшой эффект вращения во время затмения (около 70 км/с). Возможное объяснение состоит в том, что система окружена разреженным облаком, внутренние части которого вращаются вместе со звёздами, а на внешние части орбитальное движение почти не оказывает влияния. Тогда наблюдаемая скорость К-линии является средним значением лучевой скорости вдоль луча зрения по направлению к звезде сквозь облако. Если движения частиц в облаке вблизи каждой звезды приближаются к кеплеровой скорости, то наблюдаемое влияние вращения можно использовать для определения радиуса эффективного поглощающего слоя в облаке. Он оказывается примерно в четыре раза больше радиуса звезды. Чтобы получить это значение, нужно иметь сносные данные о массе и радиусе главной звезды, но окончательный результат к ним не очень чувствителен. Одним из аргументов против этой гипотезы является то, что в спектре такого огромного облака должны быть видны линии, чувствительные к дилюции излучения. Однако радиус гипотетического облака можно уменьшить, если предположить, что оно состоит из частиц, двигающихся по спирали по направлению к звезде с. меньшей, чем кеплерова, скоростью.
О деформации кривой лучевых скоростей SX Кассиопеи, подобной кривой U Цефея, уже упоминалось. Система RX Кассиопеи содержит две звезды, почти равные по светимости, и орбитальные элементы определялись из спектров обеих. Элементы не совпадают: спектр G указывает на круговую орбиту, в то время как спектр А даёт кривую лучевых скоростей, деформированную по типу Алголя. Измеренные скорости UX Единорога показывают большой разброс относительно кривой, которая соответствовала бы круговой орбите, не очень отклоняясь от результатов наблюдений. Кривая лучевых скоростей, возможно, несколько деформирована.
Системы, содержащие массивные звёзды раннего класса. В этой группе систем мы сталкиваемся с иным видом деформации кривой лучевых скоростей. У многих систем видимы оба спектра, и кривая лучевых скоростей главной (более яркой) компоненты, по-видимому, хорошо определяется и не деформирована. Однако кривая лучевых скоростей спутника совсем непохожа на кеплерову: отдельные наблюдения показывают для половины периода широкий разброс относительно примерно постоянной скорости и такой же разброс относительно другого постоянного значения для второй половины периода. Хорошим примером может служить кривая лучевых скоростей HD 190967 (рис. 8.5). Постоянные значения таковы, что скорость спутника колеблется в противофазе со скоростью главной компоненты, но значения V0 у обеих звёзд кажутся разными. Системы такого типа рассматривал Сахаде [407]; группа включает АО Кассиопеи, β Скорпиона, HD 190967 (V 448 Лебедя) и HD 47129. Поскольку две звезды одной и той же системы не могут иметь различные значения V0, Сахаде предположил, что спутник (он считает, что это – более массивная звезда, хотя её светимость меньше) заполняет свою полость Роша и окружён расширяющимся облаком газа. Линии поглощения спектра этого облака сливаются с теми же линиями спектра спутника, так что фактически измеряются линии, имеющие постоянное фиолетовое смешение относительно соответствующих линий спектра главной звезды. Такое же различие в значениях V0 имеют другие системы с большой массой: HD 217312 [164] и HD 209481 [349]. Гипотеза Петри, объясняющая этот результат ошибкой при решении орбитальных элементов методом наименьших квадратов, описывается в гл. 1. Кривая лучевых скоростей спутника у HD 209481 не так явно деформирована, как у систем, рассмотренных Сахаде; оба объяснения скорее дополняют друг друга, чем противоречат друг другу. Постулированное Сахаде облако, окружающее спутники, может также объяснить, почему они имеют меньшую светимость, чем главные звёзды, хотя и являются более массивными. Предположение Сахаде, что массы спутников больше, подтверждается тем, что значения масс, которые он получил, исходя из этого допущения, находятся в разумном согласии с теоретическими предсказаниями. Он также считает, что к системам этого типа относится β Лиры. В её спектре линии излучения оболочки так искажают профили линий водорода и гелия, что надёжные кривые лучевых скоростей можно построить только по линиям ионизированного кремния.
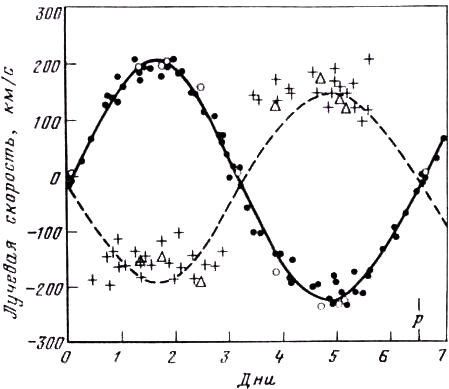
Рис. 8.5. Кривая лучевых скоростей HD 190967, иллюстрирующая тенденцию "вторичной компоненты" к постоянной лучевой скорости в обоих узлах [347].
Абхианкар [1] наблюдал несколько систем этого типа и нашёл, что в АО Кассиопеи изменяются как K1 так и K2. Амплитуды линий водорода отличаются от амплитуд линий гелия. Наибольшая деформация кривой лучевых скоростей была замечена у массивной двойной φ Персея [197]; возможно, что, по крайней мере частично, она была вызвана комбинацией профилей линий излучения и поглощения. Эта характерная система не привлекла заслуживаемого ею внимания; впрочем результаты новых наблюдений докладывались Хёрдом.
Системы типа W Большой Медведицы. Очень трудно выполнить и правильно интерпретировать спектроскопические наблюдения систем типа W Большой Медведицы. Периоды коротки, а большинство систем так слабо, что их трудно пронаблюдать с подходящим временным разрешением. Таким образом, видимые изменения значений K1 и K2 могут оказаться просто ошибками. Биннендейк [53] нашёл подобные изменения у самой W Большой Медведицы. Другая спектроскопическая проблема заключается в том, что линии в спектрах обычно подвержены значительному расширению вследствие вращения. Поскольку большая часть звёзд в этих системах принадлежит к поздним спектральным классам, расширение вращением, по-видимому, вызывает много необычных бленд в этих богатых нитями спектрах. Если бленды не распознаны и не учтены, то это может вводить систематические ошибки в измерения лучевых скоростей; значения, найденные для V0, могут очень сильно зависеть от выбора спектральных линий. Линии, но которым получают надёжные лучевые скорости в нормальных спектрах того же класса, необязательно приведут к таким же результатам в спектрах систем типа W Большой Медведицы. Биннендейк также обсуждал этот вопрос. Итак, хотя сообщалось об изменениях K1, K2 и V0 у многих систем, эти изменения нельзя безусловно приписывать влияниям Околозвездного вещества.
Катаклизмические переменные. Кривые лучевых скоростей катаклизмических переменных также очень трудно получить. Часто они основываются на одной или двух линиях излучения, нередко чрезмерно широких. Отдельные наблюдения могут показывать такой большой разброс, что невозможно сказать, деформирована или нет кривая лучевых скоростей. Системой, показавшей различия между кривыми лучевых скоростей, построенных по различных линиям, является Новая DQ Геркулеса. Линия излучения Hβ практически совсем не показывает изменения скорости, линия излучения Нγ имеет незначительное изменение; а линии Бальмера, более высокие, чем Нγ, и линия λ 4686 He II характеризуются вариациями скорости с амплитудой К= 150 км/с. Вдобавок во время затмения линия Не II расширена вращением [249]. Крафт [245] интерпретировал эти наблюдения следующим образом: эмиссия Нβ возникает в туманности, выброшенной при вспышке новой, равно как и запрещённые линии [O II] и [S II]. Эмиссия в Нγ, как он считает, возникает частично там же, а частично в более плотном диске, окружающем более горячую звезду и движущемся с ней по орбите. Предполагается, что выброшенная туманность имеет высокий бальмеровский декремент и излучение высших членов серии Бальмера и λ 4686 возникает целиком в плотном диске. Поскольку влияние вращения начинается и кончается с главным затмением, затмевается, по-видимому, скорее диск, чем сама звезда. Диск может давать значительный вклад в непрерывное излучение системы в результате свободно-свободных и свободно-связанных переходов внутри его.
У системы V Стрелы также разные спектральные линии дают различные кривые лучевых скоростей. Скорости, полученные по измерениям линий О IV, отличаются от полученных по линиям O III и обе отличаются от скоростей, измеренных по линиям водорода. Имеются некоторые указания на то, что в этой системе происходит выброс вещества по спирали, очень сходный с установленным Койпером [265] для β Лиры. Эти результаты были получены Хёрбигом и др. [171].
1. Abhyankar K.D., Astrophys. J. Suppl., Ser. 4, 157 (1959).
3. Abt H.A., Astrophys. J., 130, 769 (1959).
29. Barr J.M., J. Roy. Astron. Soc. Can., 2, 70 (1908).
38. Batten A.H., Publ. Dom. Astrophys. Obs., 13, No. 8 (1967).
39. Batten A.H., J. Roy. Astron. Soc. Can., 62, 344 (1968).
47. Batten A.H., Ovenden M.W., Publ. Astron. Soc. Рас., 80, 85 (1968).
51. Biermann P., Astron. Astrophys., 10, 205 (1971).
53. Binnendijk L., Publ. Dom. Astrophys. Obs., 13, 27 (1967).
116. Evans Т.L., Mon. Not. Roy. Astron. Soc, 141, 109 (1968).
117. Fernie J.D., Astrophys. J., 130, 611 (1959).
118. Fernie J.D., Astron. J, 71, 119 (1966).
142. Горбацкий В.Г., Астрофизика, 4, 209 (1968).
149. Günther O., Astron. Nachr., 285, 97, 105 (1959).
155. Hansen H.K., Publ. Astron. Soc. Рас. 81, 540 (1969),
156. Hansen H.K., McNamara D.H., Astrophys. J., 130, 791 (1959).
158. Hardie R.H., Astrophys. J., 112, 542 (1950).
164. Heard J.F., Fernie J.D., J. Roy. Astron. Soc. Can., 62, 99 (1968).
171. Herhig G.H., Preston G.W., Smak J., Paczynski В., Astrophys. J., 141, 615 (1965).
197. Hynek J. A., Contr. Perkins Obs., No. 14 (1940).
245. Kraft R.P., Astrophys. J., 130, 110 (1959).
249. Kraft R.P., Greenstein J.L., Astrophys. J., 130, 99 (1959).
253. Kříž S., Bull. Astron. Inst. Czech., 21, 211 (1970).
265. Kuiper G.P., Astrophys. J., 93, 133 (1941).
301. McNamara D.H., Astrophys. J., 114, 513 (1951).
347. Petrie R.M., Publ. Dom. Astrophys. Obs., 10, 259 (1955).
349. Petrie R.M., Publ. Dom. Astrophys. Obs., 12, 111 (1962).
364. Plavec M., Bull. Astron. Inst. Czech., 17, 295 (1966).
366. Plavec M., in The Determination of Radial Velocities and their Applications, eds. A.H. Batten, J.F. Heard, Academic Press, London and New York, 1967, p. 229.
407. Sahade J., in Symposium on Stellar Evolution, ed. J. Sahade, La Plata Observatory, 1962, p. 185.
412. Savedoff M.P., Astron. J., 56, 1 (1951).
426. Shobbrook R.R., Herbison-Evans D., Johnston I.D., Lomb N.R., Mon. Not. Roy. Astron. Soc., 145, 131 (1969).
428. Simon N.R., Stotkers R., Astron. Astrophys., 6, 183 (1970).
434. Smak J., Publ. Astron. Soc. Рас., 76, 210 (1964).
452. Struve O., Mon. Not. Roy. Astron. Soc., 109, 487 (1949).
456. Struve O., Huang S.-S., Occasional Notes Roy. Astron. Soc., 3, 161 (1957).
469. Thackeray A.D., Tatum J.В., Publ. Dom. Astrophys. Obs., 13, 19 (1966).
481. Van den Bos W.H., Publ. Astron. Soc. Рас., 74, 297 (1962).
488. Van Hoof A., Kleine Veröff. Remeis Sternw., 4, 149 (1965).
489. Van Hoof A., in Determinantion of Radial Velocities and their Applications, ed. A.H. Batten, J.F. Heard, Academic Press, London and New York, 1967, p. 237.
520. Wood D.B., Forbes J.E., Astron. J., 68, 257 (1963).
528. Worley C.E., Publ. Astron. Soc. Рас., 78, 485 (1966).
Дата установки: 23.02.2007
Последнее обновление: 19.11.2011
[вернуться к содержанию сайта]