[вернуться к содержанию сайта]
В начале настоящей главы был намечен подход, позволяющий описывать распространение электромагнитных волн с помощью интегральных уравнений, а в последующих разделах были введены вспомогательные величины, необходимые для этой цели. Теперь мы сформулируем эти интегральные уравнения и рассмотрим некоторые их следствия, что можно сделать, оставаясь полностью в рамках макроскопической теории, излагаемой на протяжении данной книги. В рамках этой теории интегральные уравнения эквивалентны уравнениям Максвелла и представляют собой математическое описание электромагнитных явлений с помощью взаимодействий на конечных расстояниях (им, конечно, необходимо время для распространения). Определённые преимущества такого подхода, который в ряде случаев оказывается мощнее обычного подхода, основанного на дифференциальных уравнениях, заключаются в том, что он связывает макроскопические явления с молекулярными, рассмотренными в предыдущем разделе.
Как мы уже говорили выше, можно считать, что молекулы, составляющие вещество, ведут себя в поле падающих волн подобно диполям. При этом все излучаемые диполями волны действуют на любой другой диполь с эффективной силой и определяют среднее измеряемое поле. Предположим, что диполи равномерно распределены по среде, и среднее значение их электрического момента в единице объёма Р будем рассматривать как основную величину, На самом же деле распределение молекул в среде никогда не бывает совершенно равномерным (т. е. имеются флуктуации плотности) и, следовательно, электрический момент отдельных частиц флуктуирует около среднего значения. Возникающие явления настоящая теория может объяснить, проводя расчёты несколько дальше, т. е. рассчитывая не только средние величины, но и их среднеквадратичные отклонения. Подобные расчёты важны для некоторых проблем, например для объяснения голубого цвета неба, впервые данного Рэлеем 2). Но такое распространение теории здесь провести невозможно 3).
2.4.1. Основное интегральное уравнение. Рассмотрим распространение электромагнитной волны в однородной изотропной немагнитной среде. Электрическое и магнитное поля Е'j и H'j, которые действуют на j-й диполь внутри среды, можно разделить на поля падающей волны Е(i), Н(i) (распространяющиеся со скоростью света в вакууме с) и вклад, создаваемый всеми диполями, т. е.
![]()
здесь суммирование распространяется на все диполи, кроме j-го. В точке rj, где расположен j-й диполь, поле от 1-го диполя можно определить из формул (2.2.49) – (2.2.51), а именно
![]()
где рi(t) – момент i-го диполя, Rji=|rj–ri| и операция rot производится относительно координат xj, yj, zj j-го диполя.
Как мы уже говорили, распределение можно с хорошим приближением считать непрерывным, т. е. момент диполей можно рассматривать как непрерывную функцию координат (и времени) p=p(r, t). Концентрацию N также будем считать непрерывной функцией координат N(r). В этом случае полный электрический диполыгый момент Р единицы объёма определяется формулой (2.3.14), т.е.
![]()
По причинам, изложенным в § 2.3, мы пренебрегли вкладом в (3) силы, создаваемой магнитным полем. Поскольку допускается также, что вещество немагнитно (т. е. М=0), в устанавливаемые ниже условия динамического равновесия не будет входить эффективное поле Н'.
Если подставить (2) в (1) и перейти к непрерывному распределению, используя (3), то получим 4)
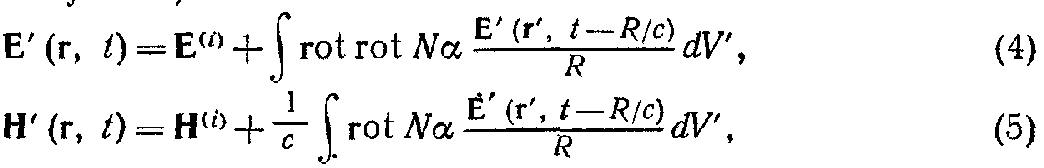
где R=|r–r'|.
Если точка наблюдения r находится вне рассматриваемой среды, интеграл берётся по всей среде. Если она расположена внутри среды, то необходимо вначале исключить небольшую область, занятую атомом; будем считать эту область небольшой сферой σ радиуса a. В конечном счёте мы обычным образом перейдём к пределу a→0.
Уравнение (4) представляет собой интегро-дифференцилльное уравнение относительно Е'. Если решить его, то можно получить Н' из (5). Эти два уравнения, по существу, эквивалентны уравнениям Максвелла для изотропных немагнитных веществ. Обобщение на магнитные среды можно провести с помощью второго вектора Герца.
2.4.2. Теорема погашения Эвальда–Озеена и строгий вывод формулы Лорентц–Лоренца. Уравнение (4) связывает довольно сложным образом эффективное электрическое поле с электрическим полем падающей волны. Это уравнение решается в явном виде лишь в специальных случаях. Тем не менее из него можно получить ряд основных результатов, таких, как формула Лорентц–Лоренца, законы преломления и отражения и формулы Френеля. Перед тем как показать это, выведем одно важное общее следствие решения.
Пусть Σ обозначает границу рассматриваемой среды. Для точек наблюдения, находящихся внутри среды, основное уравнение (4) можно записать в виде
![]()
где Е(d) – вклад от диполей, равный
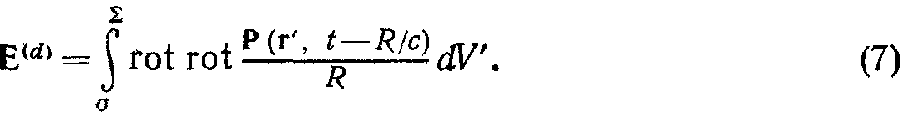
Здесь мы явно указали границу объёма, по которому проводится интегрирование.
Будем считать, что поле Е(i) создаётся падающей монохроматической волной с угловой частотой ω, т. е.
![]()
В качестве пробного решения для Р выберем волну, которая также монохроматична и имеет ту же частоту, но обладает другой скоростью распространения (скажем, c/n)
![]()
где, как и раньше, k0=ω/c и
![]()
Постоянный множитель (n2–1)k02 в (9) введён для упрощения последующих формул. Постоянную n следует рассматривать как неизвестную величину, причём её определение является одной из главных задач настоящего анализа.
Предположим также, что внутри среды
![]()
На первый взгляд возможность решения основного интегро-дифференциального уравнения (6) в форме нашего пробного решения может показаться до некоторой степени странной, так как Е(i) представляет волну, распространяющуюся со скоростью света в вакууме c, тогда как P, по предположению, распространяется со скоростью c/n. Однако будет показано, что поле диполей Е(d) можно выразить в виде суммы двух членов, один из которых удовлетворяет волновому уравнению в вакууме и в точности гасит падающую волну, тогда как другой удовлетворяет волновому уравнению для распространения со скоростью c/n. Поэтому можно считать, что падающая волна гасится в любой точке внутри среды в результате интерференции создаваемого ею поля с полем диполей; при этом появляется новая волна с иной скоростью распространения (а в общем случае и с иным направлением распространения). Найденный результат известен как теорема погашения; он был установлен вначале для кристаллических сред Эвальдом [24] и для изотропных сред Озееном [17].
Чтобы доказать теорему погашения, перепишем (6) в форме, не зависящей от времени
![]()
где
![]()
и
![]()
В приложении 5 показано, что если радиус сферы σ достаточно мал, то
![]()
Здесь функция G представляет сферическую волну в вакууме и поэтому удовлетворяет волновому уравнению
![]()
Таким образом, из уравнений (10) и (16) следует, что член, стоящий под знаком интеграла в правой части (15), можно записать в виде
![]()
При интегрировании с помощью теоремы Грина это даёт
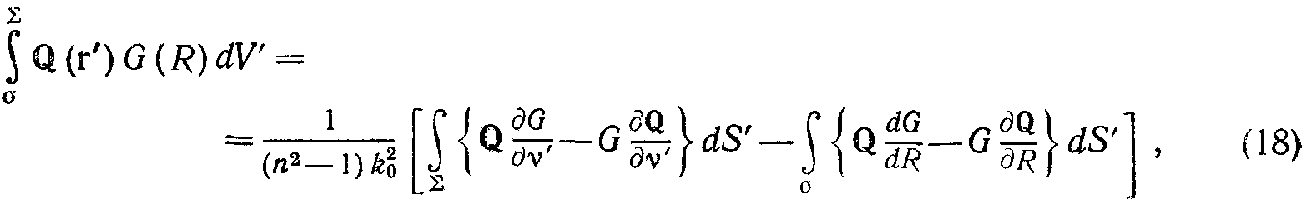
где символ ∂/∂ν' означает дифференцирование вдоль внешней нормали к границе Σ. Прямой расчёт показывает (см. п. 8.3.1), что предел поверхностного интеграла по σ при а→0 равен –4πQ(r) и, следовательно,
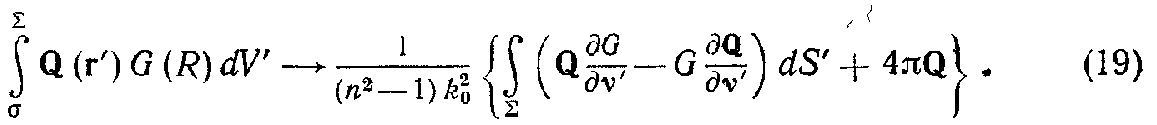
В пределе из (13), (15) и (19) получим
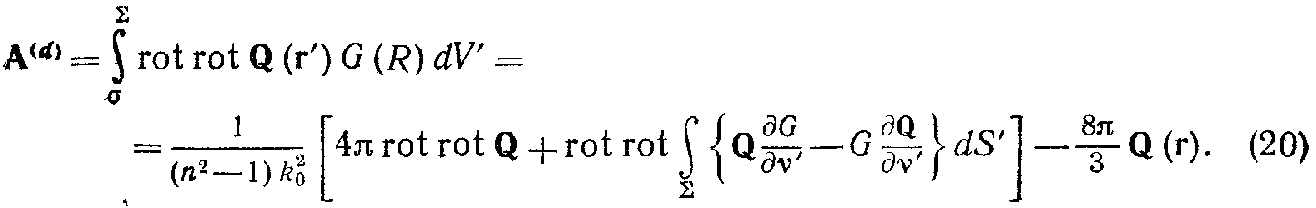
Используем далее тождество
![]()
Первый член в правой части исчезает из-за условия (11), а второй, согласно (10), равен n2k02Q. Следовательно, при подстановке их в (20) окончательно получим следующее выражение для поля диполей:
![]()
Согласно (10) первый член в правой части представляет волну, распространяющуюся со скоростью c/n, тогда как второй – волну, которая, подобно G, распространяется со скоростью света в вакууме c. Следовательно, как мы и ожидали, основное уравнение (12) разделяется на две группы членов, каждая из которых представляет волну, распространяющуюся со своей скоростью. Это возможно, только если каждая группа в нём равна нулю, и, следовательно,
![]()
и
![]()
Соотношение (23) выражает погашение падающей волны
![]()
в любой точке внутри среды, возникающее вследствие интерференции с частью поля диполей. Падающая волна заменяется другой, а именно волной вида
![]()
которая распространяется внутри среды со скоростью c/n. Величина n выражается в (22) через концентрацию N и поляризуемость α. В этом выражении мы узнаём формулу Лорентц–Лоренца, введённую предварительно в п. 2.3.3. Нужно отметить, что погашение падающей волны осуществляется исключительно диполями, расположенными на границе среды, а поляризация Р возникает только вследствие взаимодействия соседних диполей.
В принципе общее решение интегро-дифференциального уравнения (23) можно получить, приведя его к системе двух связанных интегральных уравнений Фредгольма для Q и ∂Q/∂ν' на поверхности. Тогда величину Q в любой точке внутри среды можно получить, решая уравнение (10) при условии, что Q принимает указанные значения на границе. Это нетрудно сделать обычными методами, используя функции Грина или интегральную формулу Гельмгольца–Кирхгофа (см. уравнение (8.3.7)).
Мы должны теперь связать эффективное поле Е' с обычным полем Е теории Максвелла. Для этого запишем два определения электрического смещения D, а именно
![]()
и
![]()
Исключая из них D, найдём
![]()
Теперь из (3) и (22) получим
![]()
и, следовательно, используя (26), имеем
![]()
что согласуется с (2.3.12). Наконец, из (26) и (9) следует, что поле Е внутри среды (n≠1) задаётся формулой
![]()
Для нахождения электрического поля вне среды мы должны вернуться к уравнению (4). Интегралы, входящие в уравнения (4) и (5), теперь берутся по всей среде, так что оператор rot rot можно вынести из-под знака соответствующего интеграла. Далее, так как вне среды D=Е, то Р=0 и, следовательно, согласно (27), мы формально получим Е'=Е. Вместо (6) теперь мы находим
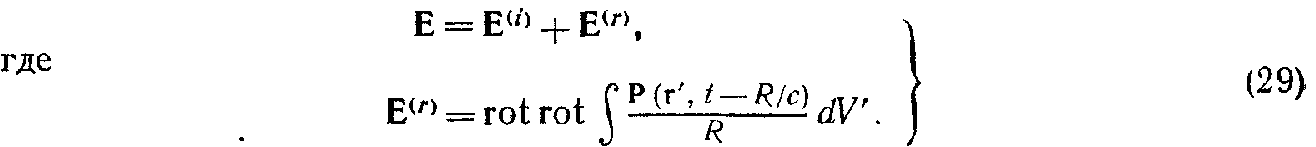
Для рассматриваемого здесь случая гармонической зависимости от времени получим, подставляя сюда выражение (9) и используя (17) и теорему Грина, соотношение
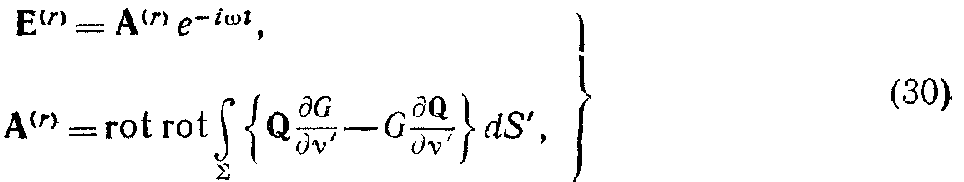
a Q – та же функция на поверхности Σ, что и раньше.
До сих пор мы занимались только электрическим полем. Для нахождения магнитного поля нужно лишь подставить Е' в (5) и взять интеграл. Это можно сделать методом, аналогичным приведённому выше, но такая операция сейчас несколько проще, так как оператор rot в (5) можно вынести из-под знака интеграла, что следует из результатов, изложенных в приложении 5. При сравнении получающихся выражений для H и для E мы увидим, что найденные решения согласуются с уравнениями Максвелла. Мы не будем приводить здесь эти расчёты, поскольку они довольно просты и не вносят каких-либо важных новых особенностей.
Чрезвычайно интересно отметить, что подход, основанный на физическом соображении о том, что поле в среде более естественно характеризовать поляризацией, чем вектором смещения, очень изящно, через интегро-дифференциальное уравнение (4), приводит к строгому выводу формулы Лорентц–Лоренца и теоремы погашения. Этот мощный метод до сих пор слабо использовался при рассмотрении более частных проблем 5); пример его применения будет дан в гл. 13.
2.4.3. Рассмотрение преломления и отражения плоской волны с помощью теоремы погашения Эвальда–Озеена. Применим теперь теорему погашения Эвальда–Озеена, выраженную формулой (23), к случаю плоской монохроматической волны, входящей в однородную среду, которая заполняет полупространство z<0. Покажем, что из этой теоремы вытекают законы преломления и отражения, а также формулы Френеля.
Падающую волну запишем в форме
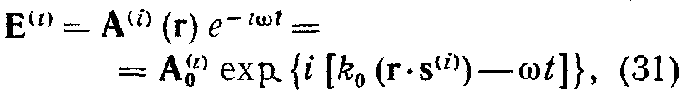
где k0=ω/c, A0(i) – постоянный вектор и s(i) – единичный вектор в направлении распространения.
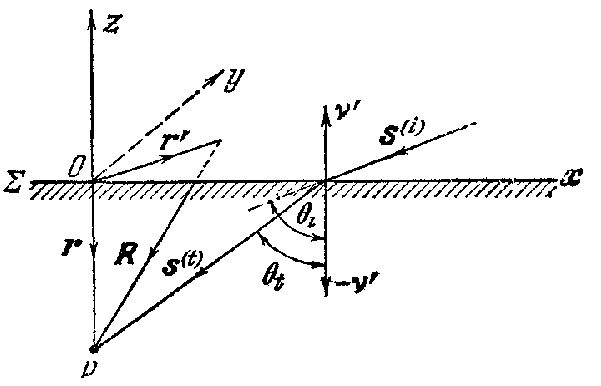
Рис. 2.4. Проникновение волны в однородную среду, рассматриваемую как система диполей.
Выберем ось z так, чтобы она проходила через точку наблюдения p, которую мы вначале считаем находящейся внутри среды на расстоянии r от границы Σ (рис. 2.4). Ось x выбираем так, чтобы вектор s(i) лежал в плоскости xz. Следовательно, обозначая угол падения через θi, мы получим
![]()
В соответствии с результатами предыдущего раздела, предположим, что прошедшая волна имеет ту же частоту, что и падающая, но другую скорость c/n, где n выражается через поляризуемость и плотность с помощью формулы Лорентц–Лоренца. В качестве пробного решения для прошедшей волны выберем плоскую волну, распространяющуюся в направлении единичного вектора s(t), который, по предположению, лежит в плоскости xz:
![]()
Тогда выражение (28) примет вид
![]()
где Q0 – постоянный вектор, который, согласно (11), ортогонален s(t).
Решение интегро-дифференциального уравнения легко получить, если рассматривать лишь точки наблюдения p, отстоящие от границы r=0 на расстояниях, больших по сравнению с длиной волны, т. е. если
![]()
Это условие наложено лишь для упрощения расчётов и не соответствует ограничению физической обоснованности интегро-дифференциального уравнения.
Производные, входящие в интеграл по Σ, теперь имеют вид
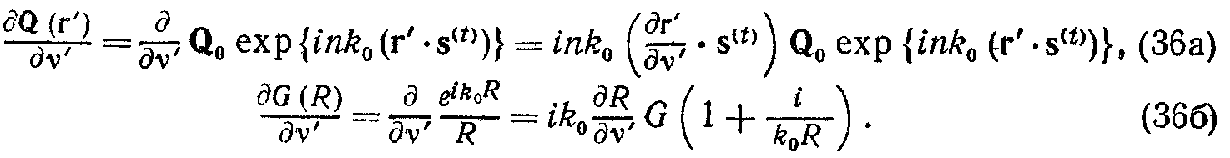
Последним членом в (36б) можно пренебречь из-за условия (35), и интеграл, входящий в (23), записывается следующим образом:
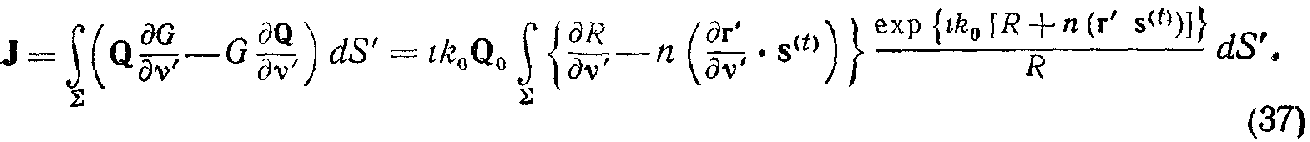
Компоненты векторов r, r' и R равны (см. рис. 2.4)
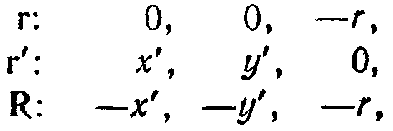
следовательно,
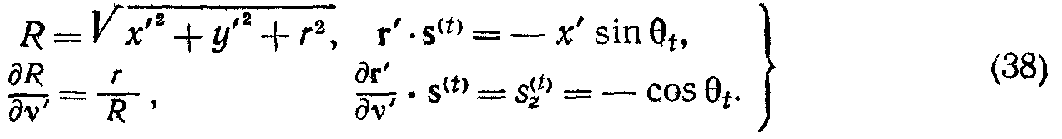
Интеграл (37) после подстановки примет вид
![]()
Удобно ввести угол φ и соответствующий единичный вектор s, определяемые выражениями
![]()
Так как, по предположению, k0r велико по сравнению с единицей, показатель степени экспоненциального члена в (39) также велик по сравнению с единицей и этот член будет быстро осциллировать и много раз менять знак, когда точка (x', y') будет пробегать область интегрирования. При таких условиях хорошее приближение к значению J получается путём применения следующей формулы, которая является следствием принципа стационарной фазы (см. приложение 3):
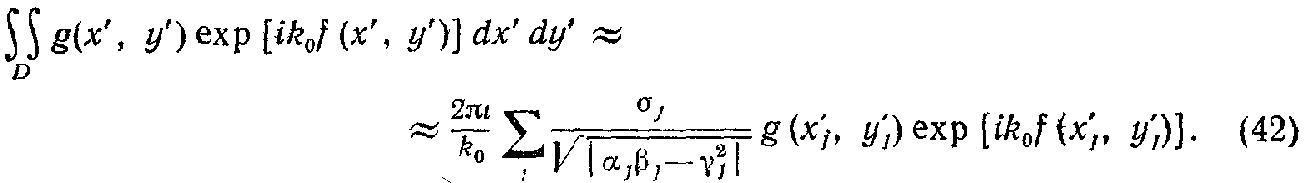
Здесь (x'j, у'j) – точки в области интегрирования D, для которых f постоянна,
![]()
и
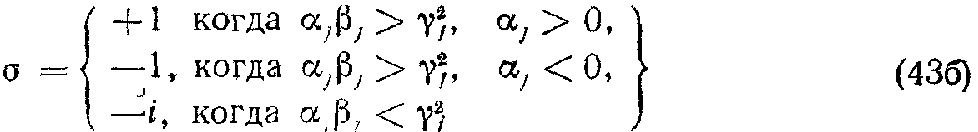
Если использовать соотношения (40) и (41), то в данном случае мы получим
![]()
и, следовательно,
![]()
Для постоянства f необходимо, чтобы
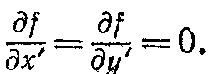
Следовательно, как легко показать (отметим, что при вычислении частных производных необходимо брать положительный квадратный корень), f будет постоянна, только если
![]()
где
![]()
В этой точке выражения (43) и (44) принимают следующие значения:

Теперь (42) примет вид
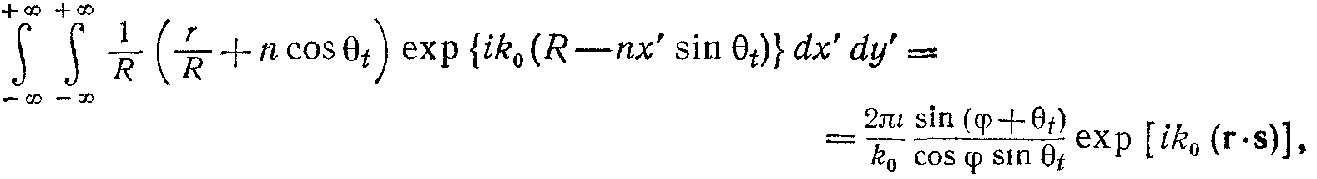
так что (39) равно
![]()
Подставив теперь это выражение в интегро-дифференциальное уравнение (23), которое выражает погашение падающей волны, получим
![]()
Следовательно, (23) перейдёт в
![]()
Это соотношение должно тождественно выполняться для всех точек r на границе. Следовательно,
![]()
и
![]()
Уравнение (49) выражает закон преломления (1.5.8). В самом деле, он означает, что
![]()
или, в соответствии с (40),
![]()
Более того, соотношения (41) и (32) показывают, что вектор s(t) лежит в плоскости, определяемой вектором s(i) и нормалью к границе Σ.
Уравнение (50) связывает амплитуды падающей волны (31) и прошедшей волны (34). Обозначая амплитуду (векторную) прошедшей волны через T0,
![]()
и раскрывая тройное векторное произведение, получим вместо (50)
![]()
Пусть A┴, A║ и T┴, T║ – составляющие А0(i) и T0 в направлениях, перпендикулярном и параллельном плоскости падения. Тогда, вспоминая, что вектор А0(i), ортогонален s(i), а T0 ортогонален s(t) и что s(i) и s(t) составляют друг с другом угол (θi–θt), найдём из (54)
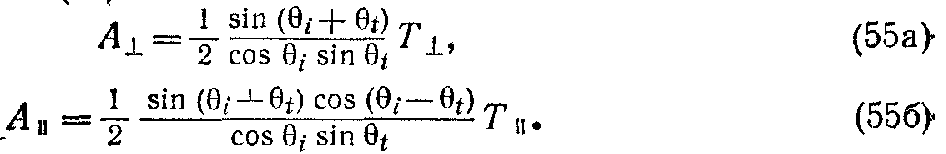
В этих соотношениях мы узнаём формулы Френеля для преломления (см. (1.5.20а)).
Наконец, рассмотрим случай, когда точка наблюдения находится вне среды (z>0). Расчёты совершенно аналогичны, только теперь в соответствующих формулах z'=–r следует заменить на z'=r. Это эквивалентно замене sz на –sz в (46г), т. е. замене φ=θi на φ=θr, где
![]()
Вместо единичного вектора s=s(i) введём теперь единичный вектор s(r) с компонентами
![]()
и получим вместо (47) соотношение
![]()
Из выражения (30) для не зависящей от времени части отражённой волны находим
![]()
Выражение (59) представляет плоскую волну, распространяющуюся в направлении, определяемом единичным вектором s(r), причём это направление связано с направлением s(i) падающей волны соотношением (56). Соотношение (56) выражает закон отражения в согласии с (1.5.7). Амплитуда А0(r) отражённой волны, выраженная через амплитуду прошедшей, записывается в виде
![]()
Обозначая через R┴ и R║ составляющие А0(r) в направлениях, перпендикулярном и параллельном плоскости падения, и используя (55), получим
![]()
и
![]()
Соотношения (61) совпадают с формулами Френеля для отражения (1.5.21а),
Некоторые обобщения этой теории, учитывающие нелинейное поведение среды (проявляющееся при исключительно сильных полях), рассмотрены в работе [23].
) Позже мы будем вновь ссылаться на теорию Рэлея в § 13.5, где рассматривается рассеяние света сферическими частицами, находящимися в вакууме. Если частицы малы, зависимость интенсивности рассеянного излучения от длины волны совпадает с этой зависимостью в рассматриваемом случае спонтанных флуктуации плотности в однородной среде (а именно, обратная пропорциональность четвёртой степени длины волны). Однако, кроме этого результата, флуктуационная теория даёт также зависимость интенсивности рассеянного излучения от флуктуации плотности. ) Эта теория рассматривается, например, в § 81 книги [5]. ) Мы должны суммировать поля, а не потенциалы, т. е. в (4) оператор rot rot должен стоять под знаком интеграла, а не вне его. В самом деле, поле, действующее на молекулу и выраженное в виде (3), получается суммированием всех индивидуальных полей. Наличие особенности у полей вблизи источников ведёт к различию между суммой полей и полем, связанным с полным потенциалом (суммой потенциалов, связанных с индивидуальными полями). См. ниже соотношение (15). ) Этот метод был применён к исследованию распространения электромагнитных волн через слоистую среду в работе [25].5. M. B o r n, Optik, Springer, Berlin, 1933. (M. Б о р н, Оптика, ГНТИУ, Харьков–Киев, 1937.)
16. W. E s m a r с h, Ann. d. Physik, 42, 1257 (1913).
17. С. W. О s e e n, Ann. d. Physik 48, 1 (1915).
18. W. В о e t h e, Beitrage zur Theorie der Brechung und Reflexion, Dissertation, Berlin, 1914.
19. W. B o e t h e, Ann. d. Physik 64, 693 (1921).
20. R. L u n d b l a d, Univ. Arsskrift, Upsala, 1920.
21. С. G. Darwin, Trans. Cambr. Phil. Soc. 23, 137 (1924).
22. H. H о e k, Algcmeene theorie der optische activiteit van isotrope media, Thesis, Leiden, 1939.
23. N. В 1 о e m b e r g e n, P. S. P e r s h a n, Phys. Rev. 128, 619 (1962).
24. P. P. E w a 1 d, Dissertation, München, 1912; Ann. d. Physik 49, 1 (1916).
25. С. W. O s e e n, Ann. d. Physik 48, 1 (1915).
26. D. R. H a r t r e e, Proc. Cambr. Phil, Soc. 25, 97 (1929).
Дата установки: 26.08.2010
[вернуться к содержанию сайта]