(напечатано в журнале "Инженер" №10, 2006 г.)
Напрашивается гипотеза, что колебания в сериальных спектрах
создаются чисто магнитными силами. Далее будет показано, что это позволяет легко понять законы спектральных серий и аномальные эффекты ЗееманаВальтер Ритц [1]
Вскоре после открытия электромагнитной природы света и постройки первых излучателей и приёмников радиоволн, учёные всерьёз задумались над устройством природных излучателей света – атомов. В первой модели, предложенной Дж. Томсоном, атом предстал в виде антенны, типа металлического шарика, испускающего излучение при колебаниях электронов, вкраплённых в атом, как сливы – в пудинг. Потом пришла планетарная модель атома Резерфорда, где электроны обращались вокруг заряженного ядра, словно планеты. Но такой атом нестабилен: снующие по орбитам электроны, излучая энергию, падали бы на ядро. Этот недостаток устранила квантовая модель атома Бора – ученика Резерфорда, но такой ценой, которая и до сих пор побуждает многих искать более рационального устройства атомному мирку. Предлагают вернуться и к модели пудинга, и к планетарной. Но, оказывается, существует и третья классическая модель атома – магнитная, предложенная в 1908 г. В. Ритцем.
Собственно, именно эта модель и позволила впервые найти весь спектр частот, излучаемых атомом водорода, причём столь оригинальным путём, что он и сегодня заслуживает внимания, как показано в замечательной статье [
1]. Ритц не применял квантовых идей: электромагнитные волны в его модели генерировали не абстрактные квантовые переходы, а классические колебания электронов. Ещё до Резерфорда Ритц понял, что движением электрона в атоме управляет некий центральный механизм, остяк, скелет атома, то что сейчас называют ядром. Но Ритц, в отличие от Резерфорда, догадался, что управление это осуществляют не электрические, а магнитные силы, за что его модель атома была названа магнитной.
Мы чересчур привыкли считать, что электроны в атоме движутся по орбитам под действием электрического притяжения ядра, забывая, что сами на практике – в ускорителях частиц, в индукционных печах – создаём круговые движения электронов с помощью магнитных полей. Ритц убедительно показал, что только силами магнитной природы можно объяснить спектры излучения атомов. Согласно ему, магнитное поле атома создано набором последовательно соединённых элементарных магнитиков стандартного размера
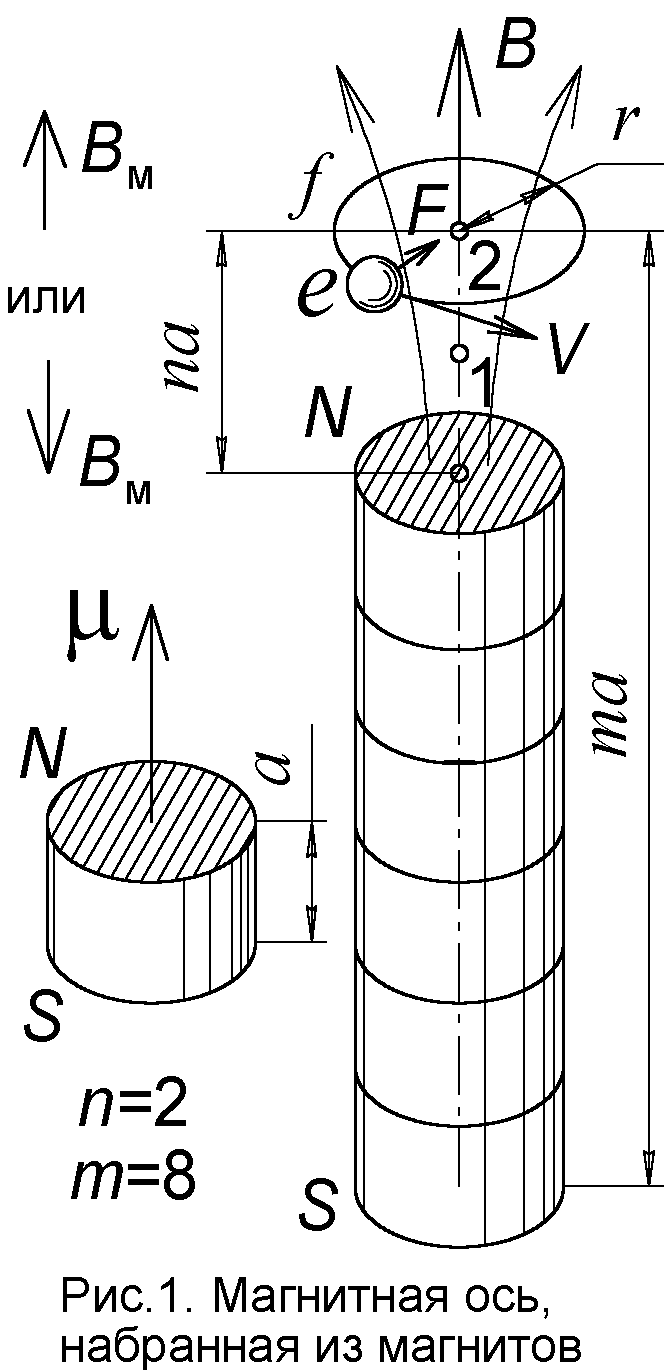
a, образующих вытянутый магнитный стержень (рис.1). Вместо магнитов можно взять витки с током, составляющие катушку индуктивности, соленоид с постоянным шагом витка a. Как показал Ритц, в зависимости от числа магнитов (витков) стержень создаёт такие магнитные поля, в которых электрон должен колебаться с теми частотами, что были найдены в спектре атома водорода.При всей наивности представления атома в виде некоего прибора (гибрида циклотрона и магнитной антенны) модель Ритца не только верно описала спектр водорода и эффект Зеемана, но и предсказала новые спектральные серии, поздней действительно найденные. Но трагическая гибель Ритца в 1909 г., спустя год после публикации его баллистической теории и модели атома, позволила о них забыть, хотя открытыми с их помощью принципами учёные не побрезговали. В свете открытий ушедшего столетия, которое не внесло ясности в квантовую модель атома, а лишь запутало её, модель атома Ритца обретает новое звучание.
Так, открыли, что у каждого электрона есть стандартный магнитный момент μ, наделяющий электрон свойствами элементарного магнитика. Тем же магнитным моментом μ обладает и открытый в XX веке антиэлектрон – позитрон. Представим теперь, что позитрон соединился с электроном, и этот диполь стал одним концом притягивать электроны, а другим – позитроны. В итоге, электроны и позитроны, последовательно цепляясь друг за друга паровозиком, могут сливаться в протяжённые прямые цепи, в которых все магнитики (магнитные моменты) электронов и позитронов ориентированны одинаково. Расстояния между их центрами окажутся постоянными, одинаковыми – порядка размера электрона
a (рис.2).
Итак, магнитные стержни, оси, набранные из элементарных магнитиков, которые Ритц только предполагал, в принципе могут образоваться сами, как линейные молекулы полимеров, построенные из тысяч одинаковых звеньев, к примеру, из чередующихся атомов Si и O (силикон). Стержни, содержащие равное число электронов и позитронов, не имели бы заряда, но породили бы заметное магнитное поле. Поэтому оказавшийся возле стержня электрон не был бы ни отторгнут, ни притянут, но мог бы совершать в магнитном поле стержня круговые движения возле точки равновесия с частотой
f, не зависящей от его скорости V и радиуса орбиты r (рис.1). В магнитном поле с индукцией B на электрон с зарядом e и массой M действует сила Лоренца F=eVB, заставляющая его двигаться по окружности с центростремительным ускорением a=V2/r. Поскольку Ma=F, имеем MV2/r=eVB, откуда угловая скорость электрона 2πf=V/r=Be/M. То есть частота f=Be/2πM обращения электрона, равная частоте излучаемого им света, зависит лишь от индукции поля B, поскольку величина e/2πM постоянна.Однако спектры излучения атомов состоят из дискретного ряда частот. Значит, и поле
B может принимать лишь определённые значения. Это заставило Ритца предположить, что электрон способен занимать в атоме лишь некоторые устойчивые положения, каждому из которых присуще своё значение поля B, задаваемое расстоянием электрона до стержня. Эту мысль о наличии в атоме устойчивых положений, орбит электрона Ритц, в отличие от Бора, развивал в рамках классического, а не квантового подхода. Он считал, что раз стандартны расстояния и размеры a магнитов, то тем же расстоянием a должны быть отделены и возможные положения электрона – узлы 1, 2, 3 ..., где он способен пребывать (рис.1).Именно так и вёл бы себя электрон возле электрон-позитронного стержня, который за счёт неравномерного (дискретного) распределения зарядов создаёт небольшое продольное электрическое поле. Поэтому, где бы ни находился электрон, он всегда стремится встать против положительного позитрона, а возникающая при смещении электрона продольная сила возвращает его на место (рис.3). То есть, электрон способен устойчиво занимать положения лишь напротив позитронов, и может "прыгать" вдоль стержня только на расстояние 2
a.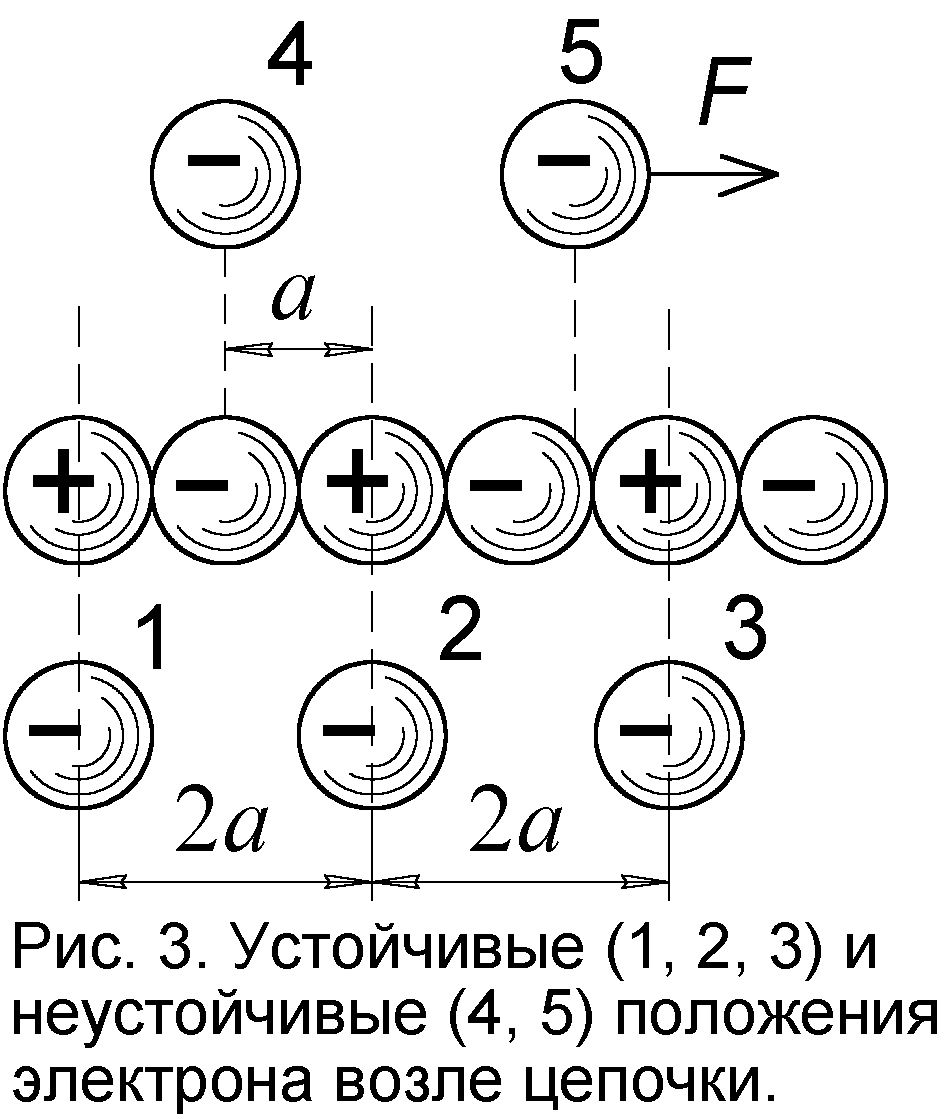
Но смещение электрона вдоль стержня не влияет на величину магнитного поля. Да и Ритц считал, что у электрона кратно а меняется расстояние до магнита. Поэтому приходим к выводу, что в атоме не один, а два стержня, две магнитных оси, соединённых перпендикулярно, наподобие перекладин креста (рис.4). Электрон, размещаясь против позитронов каждой оси, должен находиться в одном из узлов сетки, образованной линиями уровня позитронов, и его расстояние до каждого стержня будет кратно 2
a. Потому и поле B меняется прерывисто. Итак, в крестовой магнитной модели атома электрон и впрямь может занимать лишь некоторые устойчивые положения, возле которых и колеблется в магнитном поле крестовины. И что очень важно, эта дискретность вводится в рамках классической физики.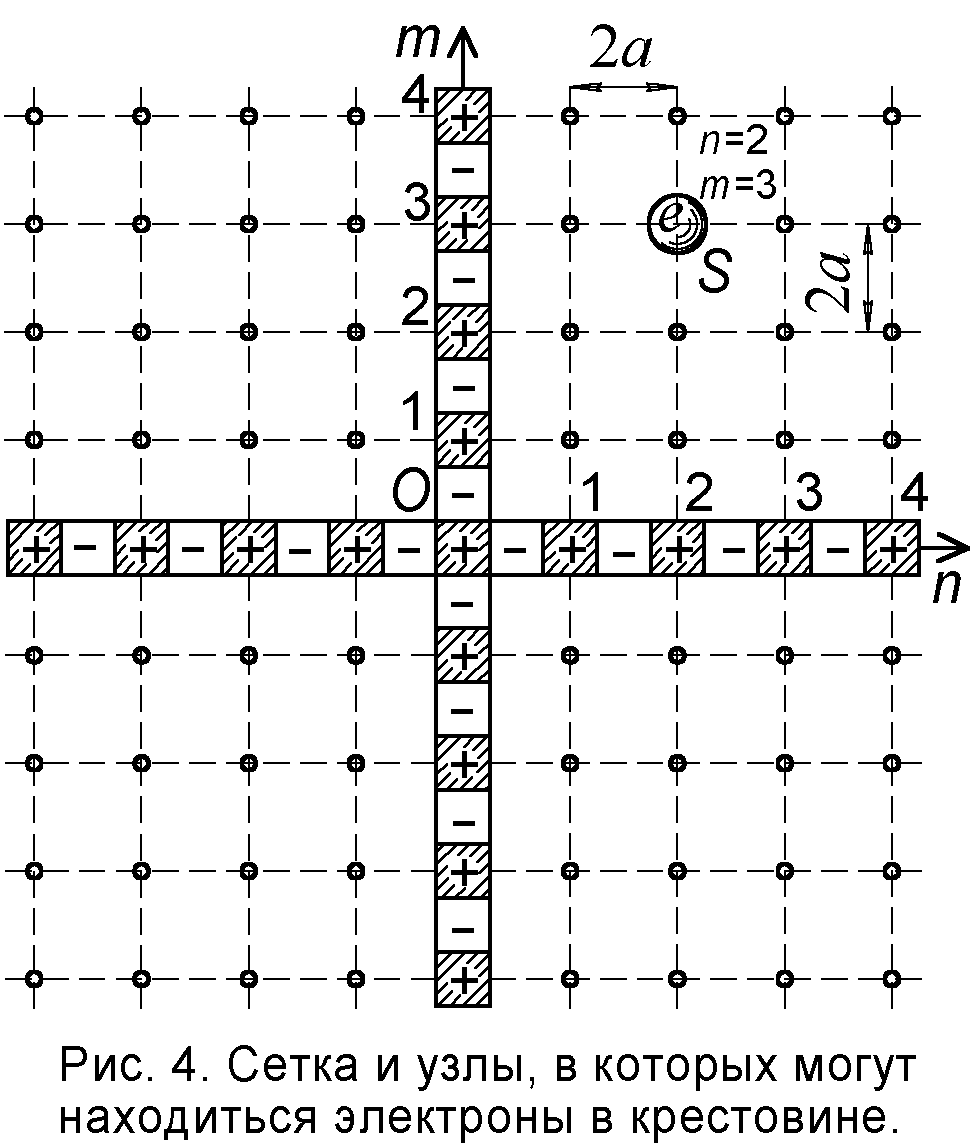
Крестовины могут нарастать так же естественно, как отдельные стержни. Крест мог бы образоваться из двух "слипшихся" стержней. Но скорее электрон-позитронные цепочки, стержни, оси и кресты растут, "кристаллизуются" от неких центров, ядер, подобно тому, как это происходит с настоящими кристаллами, дендритами. Этими центрами могут быть ядра атомов, их протоны и нейтроны. Тем более что они, как было выяснено [
2], могут содержать сколько угодно позитронов и электронов – в нейтроне их поровну, а у протона позитронов на один больше. Именно ядра могут поставлять необходимые для роста крестовины частицы.При "кристаллизации" креста, как и при росте поликристаллов железа, магнитные моменты частиц поначалу ориентируются случайным образом. Но если в одном стержне случайно окажется чуть больше частиц с моментом направленным вверх, то его магнитное поле заставит некоторые частицы второго стержня повернуться так, чтоб их моменты, ориентируясь вдоль линий поля, направились вниз. Тогда и этот стержень создаст поле, в свою очередь побуждающее больше частиц первого стержня повернуться вверх. И так постепенно, путём эдакой самоорганизации магнитные моменты обоих стержней упорядочатся, так что первый стержень образует в плоскости креста поле направленное вниз, а второй
– вверх (рис.5).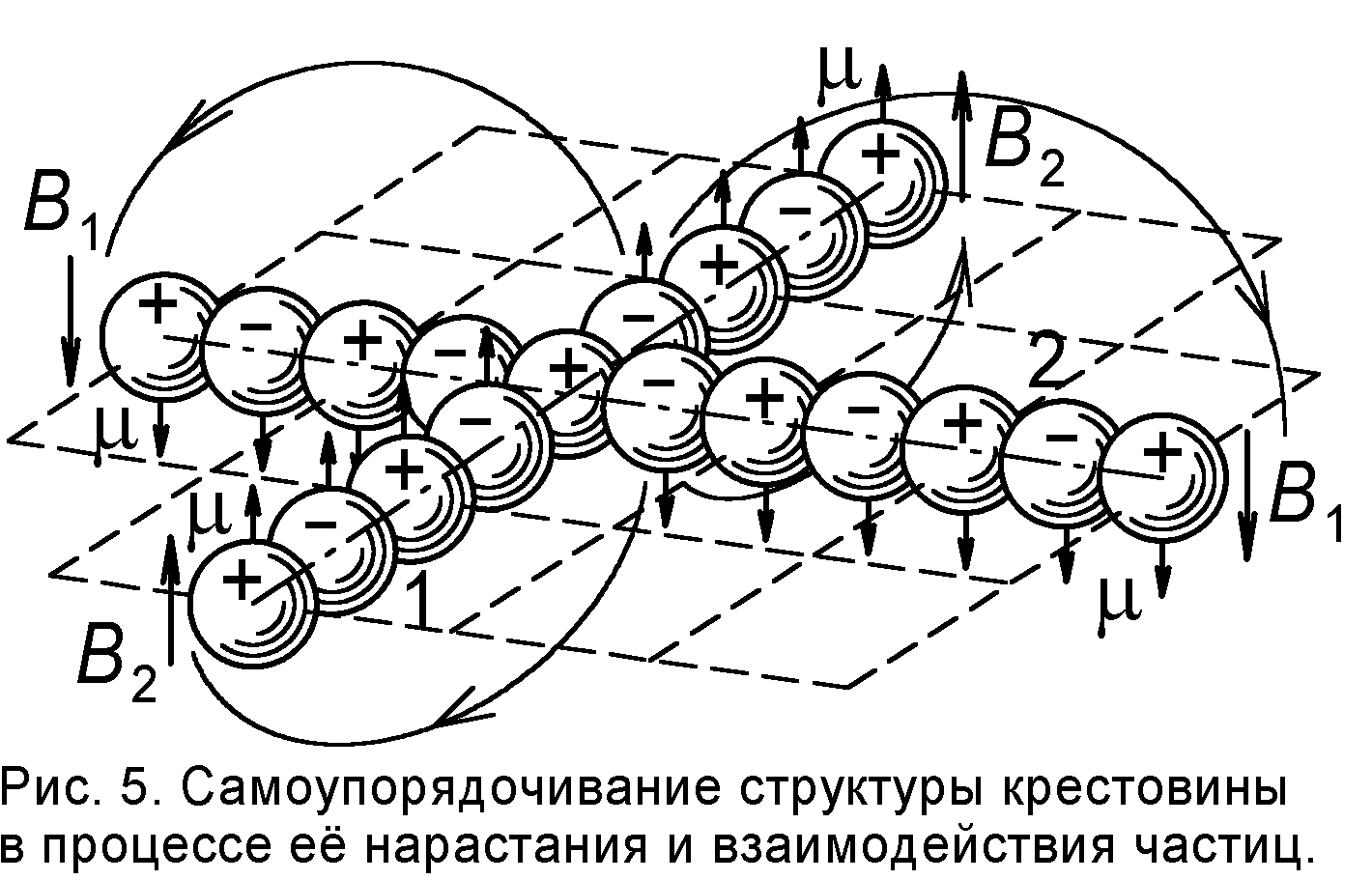
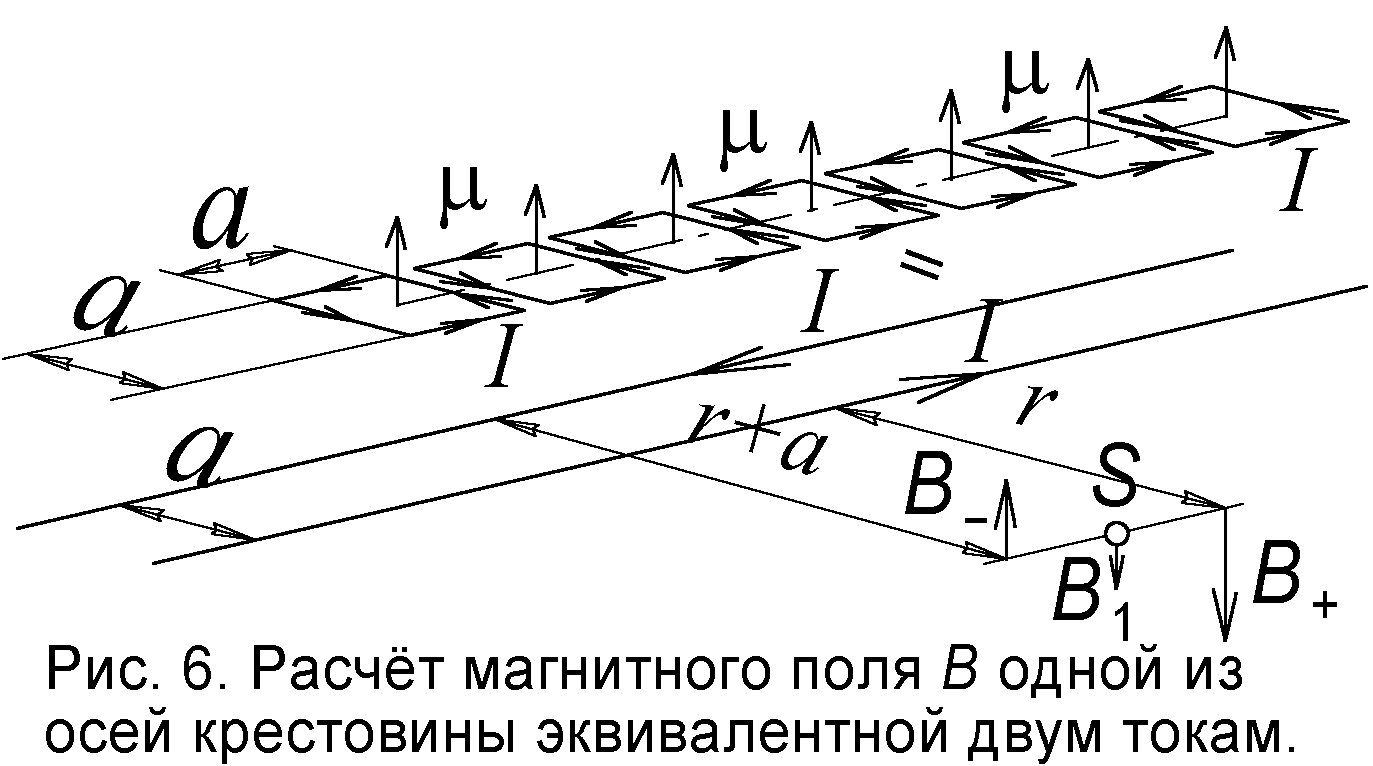
Найдём величину этого поля. Поскольку каждую частицу в цепи можно уподобить витку с током I, магнитный момент которого Ia2=μ, где a2 – площадь квадратного витка, то, будучи сложены вместе, витки дают то же поле, что у двух параллельных и противонаправленных токов I (рис.6). Один ток, находящийся от точки S на расстоянии r, создаст в ней поле B+=μ0I/2πr (μ0 – магнитная постоянная), а другой, удалённый уже на расстояние r+a, генерирует противоположно направленное поле B–=μ0I/2π(r+a). Их разность с учётом малости a даёт у первого стержня B1= μ0Ia/2πr2= μ0μ/2πar2. То же поле B2= μ0μ/2πar2, но направленное противоположно, создал бы на расстоянии r второй стержень (рис. 7). В целом на электрон, расположенный на расстоянии 2ma от первого стержня и 2na – от второго, действует поле B= B2 - B1= μ0μ/8πa3(1/n2–1/m2), где n и m – произвольные целые числа 1, 2, 3…
Соответственно частота колебаний электрона в таком поле и частота излучаемого им света f=Be/2πM=Rc(1/n2–1/m2), где постоянная R=eμ0μ/16π2ca3M. Подобную формулу Ритц и вывел в 1908 г., исходя из своей магнитной модели атома, и сформулировал на её основе комбинационный принцип, согласно которому весь набор частот, излучаемых атомом, можно получить, придавая разные целые значения величинам n и m, комбинируя их в разных сочетаниях. Так Ритц первым нашёл весь спектр частот атома водорода, даваемый известной формулой f=Rc(1/n2–1/m2), где коэффициент R носит название постоянной Ридберга.
Магнитная модель атома Ритца была первой и единственной классической моделью, позволившей объяснить спектр водорода. Поэтому совершенно неясно как могли современники Ритца, использовав результаты магнитной модели, саму её обойти стороной. Поражает простота и наглядность этой модели. Частота, с которой будет колебаться и излучать электрон, зависит исключительно от того, в каком из узлов координатной сетки атома он будет находиться. Причем числа
m и n выражают просто номер узла, как бы координату электрона вдоль соответствующей оси крестовины – этой внутриатомной системы координат, крест которой и впрямь схож с антенной, радиомачтой и крестовыми цепочками радиотелескопов. В этой модели гармонично сочетаются магнитная модель Ритца и его же ранняя модель, изображавшая атом плоской квадратной мембраной с двукратно бесконечным числом узлов [1].Магнитная модель не только объясняла спектр водорода, но и не имела пороков планетарной модели, созданной три года спустя. Излучающий электрон, кружа возле узла и теряя по мере сужения витков орбиты скорость, не упадёт на ядро, как в планетарной модели, а просто замрёт в этом узле. Когда атом, участвуя в хаотическом тепловом движении, столкнётся с другим атомом, то "взбалтывание" в нём электронов, как пассажиров в автобусе, снова придаст электрону в узле скорость. Поэтому спектральные линии тем ярче, чем выше температура газа – чем интенсивней идёт возбуждение колебаний электронов в его атомах.
Поглощение света атомом – процесс обратный. Падающая электромагнитная волна, воздействуя на покоящийся в одном из узлов электрон, сможет вызвать заметные его колебания только в том случае, если её частота
f совпадает с собственной частотой колебаний электрона в данном узле – если имеется резонанс [3]. Потому атом эффективно поглощает только те частоты, которые сам излучает. Когда воздействие излучения на атомы вещества закончится, они ещё некоторое время пребывают в возбуждённом состоянии: их электроны, набравшие скорость и кружащие в своих узлах, продолжают излучать энергию, экспоненциально убывающую. Так магнитная модель объясняет люминесценцию и фосфоресценцию.Выясним теперь, какую роль в магнитной модели играет электричество, заряд ядра. Если поле осей крестовины задаёт расположение электронов, то поле ядра – их число в атоме. В самом деле, положительный заряд ядра должен уравновешиваться отрицательным зарядом электронов, иначе атом, имеющий заряд, будет отталкивать или притягивать электроны, пока не станет нейтральным. Но хотя заряд ядра и определяет равновесное число электронов в атоме, вовсе не он
ответственен за их удержание там. Именно поэтому существуют отрицательные ионы – атомы с избытком электронов, невозможным по теории Бора. Ведь, если электроны удерживает электрическая сила, то как сможет нейтральный атом удержать лишний электрон, а тем более два или три? Даже поляризованному атому это не по силам.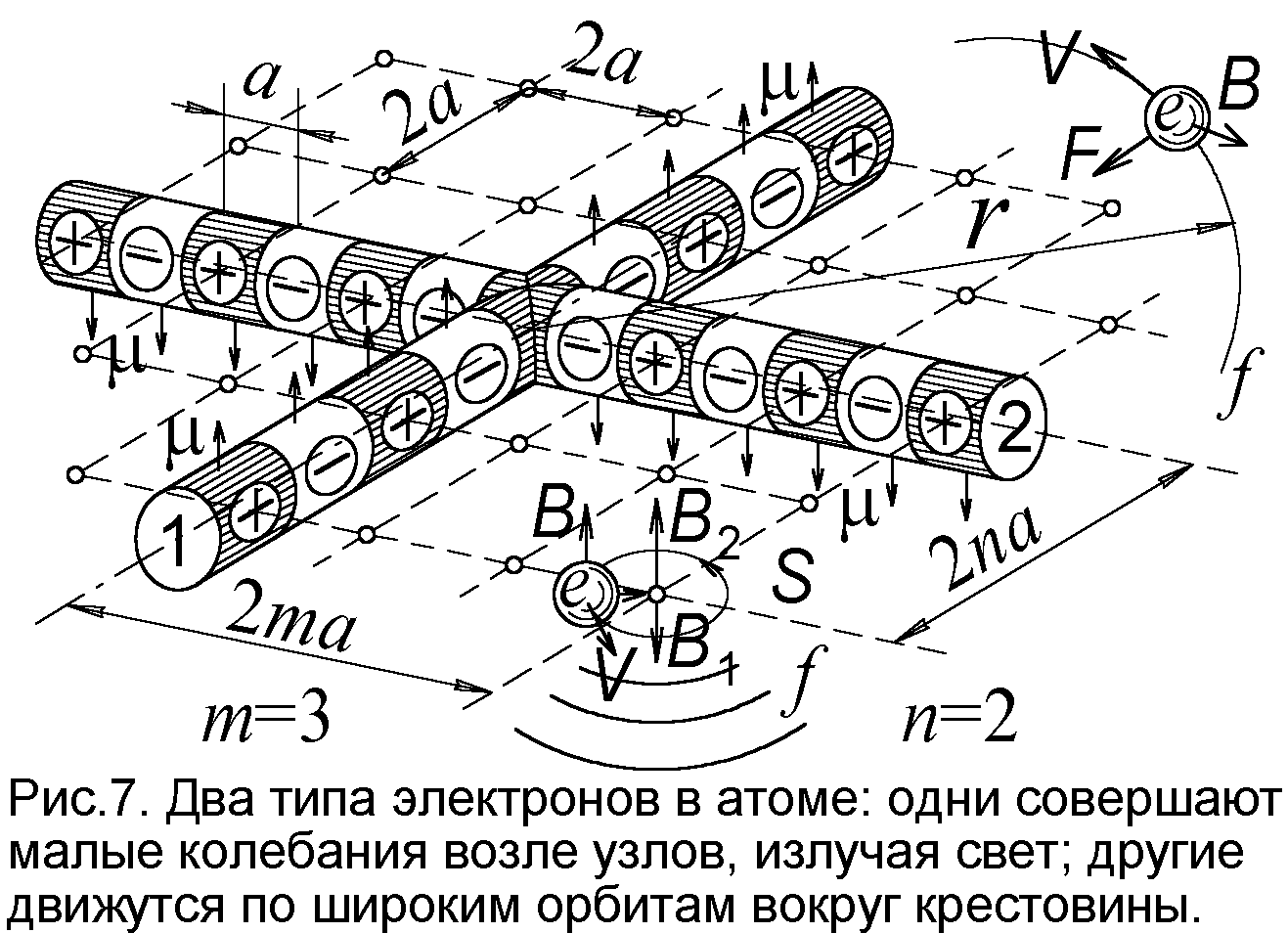
Но для магнитной модели анионы не проблема. Нейтральный атом может легко удержать лишний электрон в одном из узлов сетки. А для удержания многих электронов есть и более эффективный механизм – магнитное поле крестовины. На лишний электрон, влетающий в атом, действует сила Лоренца, способная удержать его на орбите, даже при отталкивании другими электронами (рис. 7). Таким образом, электроны в атоме делятся на те, что занимают устойчивые положения в узлах крестовины и те, что обращаются вокруг неё, удерживаемые магнитным полем. Если первые ответственны за спектры атомов, то вторые, не имеющие устойчивых орбит и положений, проявляются в фотоэффекте и эффекте Комптона.
В самом деле, как было выяснено [
3], фотоэлектроны, вырываемые из атома электромагнитной волной, уже изначально обладают орбитальной скоростью V, связанной с частотой f света и обращения электрона соотношением MV2/2= hf. Однако если б электрон удерживала на орбите электрическая кулонова сила, частота его обращения была бы пропорциональна кубу, а отнюдь не квадрату скорости V. Значит, эта сила магнитной, а не электрической природы. И действительно, в магнитном поле В на электрон действует сила Лоренца F= eVB=MV2/r. Мы выяснили, что у стержня B= μ0μ/2πar2. Поле двух осей крестовины в среднем в два раза больше. Поэтому MV2/r= eVμ0μ/πar2, откуда, домножая всё на r/2, имеем MV2/2= k(V/2πr), где V/2πr – это частота f обращения электрона, а k= eμ0μ/a– некоторая константа.Если коэффициент
k равен постоянной Планка h, то придём к общеизвестной формуле MV2/2= hf, связывающей энергию фотоэлектрона с частотой выбившего его света f. Покажем, что k=h. Для этого в формулу k= eμ0μ/a подставим известные значения магнитного момента электрона μ= eh/4πM и расстояний a между электронами и позитронами, составляющих порядка классического радиуса электрона a= e2/4πε0Mс2 (3·10–15 м) [4, 5]. Отсюда k= h/ε0μ0с2= h.Поясним, какой смысл мы вкладываем в термин "классический радиус электрона" и величину 10–15 м, которую физики называют "ферми". Надо думать, она выражает не столько размер электрона, сколько некий масштаб микромира – то расстояние, на котором исчезает электрическое взаимодействие, подобно тому как сила тяготения утрачивает своё господствующее значение при переходе от космических к микроскопическим масштабам. Так и кулонова сила на расстояниях порядка 10–15 м становится исчезающе мала либо сама по себе, либо в сравнении с силами другой природы, проявляющимися на таких расстояниях. Недаром и размеры ядер атомов составляют как раз около 10–15 м: на таком расстоянии кулоновское отталкивание протонов в ядре уже не мешает им сблизиться. Думается, по той же причине электроны в сверхпроводнике, несмотря на отталкивание, способны слипаться в так называемые куперовские пары. Так или иначе, притяжение и отталкивание зарядов на расстояниях порядка 10–15 м исчезает (или меняет знак), и это расстояние a становится равновесным.
По той же причине на таком расстоянии иначе взаимодействуют “магнитики” частиц-соседей по цепочке. Вместо того чтоб установиться противоположно, их моменты во внешнем поле ориентируются сонаправленно. Не в этом ли причина странного поведения частиц, устанавливающих спин и магнитный момент не только вдоль, но и против внешнего магнитного поля? Физики же это "объясняют" абстрактным квантованием направлений спина [4].
Проблема взаимодействия частиц с магнитным полем вплотную подводит нас к вопросу об эффекте Зеемана. В рамках своей модели Ритц легко объяснил, задолго до квантовой теории, все главные особенности эффекта Зеемана, в том числе и те, которые не позволяла понять планетарная модель атома. В самом деле, во внешнем магнитном поле магнитный момент атома установится вдоль линий поля. При этом внешнее магнитное поле
Bм, налагаясь на поле крестовины B либо увеличивает, либо уменьшает его (рис.1). Поэтому у одних электронов частота колебаний увеличится на Δf=eBм/2πM, а у других – уменьшится на ту же величину. В итоге появятся спектральные линии, смещённые вправо и влево от обычных.Итак, из классических моделей только модель атома Ритца объясняла спектральные закономерности. Правда, Ритцу пришлось для этого привлечь новые идеи – об элементарных магнитах, о масштабе длины микромира (то что теперь называют радиусом действия ядерных сил). Но XX век полностью подтвердил его предсказания: был открыт спин, магнитный момент электрона, в физику вошло ядерное взаимодействие, задающее стандарт расстояний в ядре. Всё это характеризует Ритца как смелого мыслителя, как гениального провидца с мощнейшей научной интуицией, сумевшего одной только силой мысли проникнуть и в глубь атома и в бездну космоса настолько далеко, что он опередил науку на сотню лет.
Конечно, магнитная модель атома ещё несовершенна и требует доработки. Кроме спектра водорода ей предстоит объяснить спектры других атомов. В ней надо найти место протонам, нейтронам и электронам. Последние, вероятно, расположены в узлах крестовины, как в узлах кристаллической решётки. Такое кристаллоподобное строение атома, постепенное заполнение электронами узлов по уровням
n и m позволяет естественно (не в пример квантмеху) объяснить периодичность свойств элементов. Всё это перекликается с идеями В. Мантурова [5], тоже представляющего ядра атомов в форме кристаллов, составленных из позитронов и электронов, разделённых стандартными промежутками. Кристаллические модели атома, в отличие от нестабильных динамических, показывают, что в рамках классической физики понять атомные и ядерные законы можно. А постоянно внушаемая мысль о неизбежности квантмеха для микромира – это миф и даже обман, если учесть долгое замалчивание успехов магнитной модели атома, реализованной Ритцем целиком в рамках классической механики.С.Семиков
Источники:
1. Ельяшевич М.А., Кембровская Н.Г., Томильчик Л.М.
2. О природе электричества и магнетизма // "Инженер", 2006 г., №1.
3. Свет – частица ли?// "Инженер", 2006 г., №6.
4. Матвеев А.Н. Атомная физика. М., 1989.
5. Мантуров В. Ядерные силы – предложение разгадки // "Техника-молодёжи", 2006 №2.
[вернуться к содержанию сайта]Дата установки: 28.10.2006.