[вернуться к содержанию сайта]
Измерения силы тяжести производились лишь для макроскопических предметов [
1, 2], нейтральных частиц [3] обычной материи и фотонов [4]. Моррисон и Гольд предположили возможность того, что обычная материя отталкивает антиматерию [5, 6].Косвенные данные о виртуальной антиматерии в нуклонах [
7] и о короткоживущих античастицах [8] подсказывают, что антиматерия имеет обычные гравитационные свойства, однако нет прямых измерений, подтверждающих это.Наличие отталкивающей силы представляло бы большой интерес не только потому, что это нарушило бы принцип эквивалентности общей теории относительности, но и потому, что это оказалось бы механизмом для отделения в больших масштабах материи от антиматерии во Вселенной [
5, 6].В целях исследования гравитационных свойств антиматерии было решено сравнить гравитационное ускорение позитронов и электронов в поле тяжести Земли [
9]. Настоящая статья описывает осуществление первой половины этой программы, именно определение ускорения электронов гравитационным полем Земли в вакууме внутри металлической трубы.Техника измерения силы тяжести электронов обсуждалась вкратце Витеборном, Кнайтом и Фаирбанком в [
10] и подробно Витеборном [11]. Наиболее подходящий метод заключается в анализе распределения времён пролёта свободно падающих электронов внутри металлической трубки, в которой все вертикальные градиенты электрической и магнитной потенциальной энергии меньше 10–11 эв/м, за исключением известных или умышленно наложенных однородных электрических полей. Такие однородные электрические поля должны быть порядка mg/e=5,6·10–11 в/м, где m — инертная масса электрона, g — гравитационное ускорение макроскопической нейтральной материи и е — абсолютное значение электрического заряда электрона.
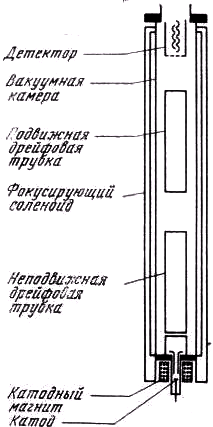
Рис. 1. Схема части установки, погруженной в гелий
Электрическая проводка, сосуд Дьюара, система вакуума не показаны. Результаты, обсуждаемые в настоящей статье, получены при отрицательном смещении неподвижной дрейфовой трубки относительно вакуумной камеры и подвижной дрейфовой трубки, так что электроны двигались медленно только в неподвижной трубке
Вертикальное электрическое поле, происходящее от индуцированных зарядов, значительно уменьшается в случае заключения зоны свободного падения в длинную (91
см) вертикальную медную дрейфовую трубку (рис. 1), с очень точным внутренним диаметром (5 см ± 0,0003 см). Электроны вынуждены двигаться вдоль оси дрейфовой трубки благодаря магнитному полю коаксиального сверхпроводящего соленоида. Дрейфовая трубка уменьшает как индуцированный потенциал, так и потенциал от зон катода и детектора приблизительно в ехр(–2,4 z/a) раз, где z — расстояние от ближайшего конца трубки и а — радиус трубки.Электрическое поле от томсон-эффекта (электродвижущая сила из-за градиента температуры) доводится до минимума термической изоляцией трубки везде, кроме одного конца, где она соединяется медными и сапфировыми стержнями с ванной жидкого гелия вне вакуумной системы. Коэффициент Томсона для меди вблизи 4,2° К порядка 10-6 в/град, так что температурный градиент меньше, чем 10-5 град/м.
Решение работать с установкой при температуре жидкого гелия обусловлено желанием пользоваться строго постоянными токами для поддержания не меняющегося со временем магнитного поля в зоне свободного падения и преимуществом криогенного откачивания. Последнее весьма важно для снижения давления ниже 10–11 торр
, чтобы взаимодействия с индуцированными диполями остаточного газа были достаточно слабыми и редкими. Наиболее важное преимущество низкой температуры заключается в бесспорном подавлении мозаичного эффекта (patch effect). Ожидалось, что пространственные флуктуации работы выхода на поверхности дрейфовой трубки, обусловленные хаотической ориентацией кристаллов (patch effect), вызовут флуктуации потенциала на расстоянии 1 см порядка 10-3 эв при комнатной температуре [11]. Оказалось, что при 4,2° К на оси дрейфовой трубки диаметром 2 см флуктуации потенциала были меньше, чем 10-10 в/м [10, 11].Возможно, это объясняется адсорбцией водорода и гелия из основного газа во время охлаждения. Эти газы достаточно подвижны, чтобы двигаться по покрытой газом поверхности при 4,2° К в сторону минимума энергии. Это может иметь результатом поверхностный потенциал, пространственные флуктуации которого имеют атомные размеры, что с очень большой вероятностью обеспечивает постоянный потенциал на протяжении нескольких сантиметров.
Предполагается, что фокусирующий соленоид создавал однородное (с точностью 10–4) магнитное поле напряжённостью в пределах 7–20 G, несоизмеримое с внешним экранированным полем, допускающим пространственные вертикальные колебания порядка 0,05 G. Взаимодействия между полем с градиентом порядка 0,05 G/м с магнитным моментом спина и орбитального движения электрона вызывают силы по крайней мере 10 mg, за исключением электронов в основном состоянии. Магнитная энергия нулевой точки орбитального движения уравновешивается с высокой степенью точности магнитной энергией спина электронов в основном состоянии. При помещении источника электронов в сильном магнитном поле (3000 G) электроны, не находящиеся в основном состоянии, испускаются с магнитной потенциальной энергией свыше 10–6 эв. Электроны в основном состоянии взаимодействуют лишь с градиентом поля, аномальный магнитный момент которого примерно в 2000 раз меньше и противоположно направлен. Итак, группа электронов, излученных катодом, становится пространственно обособленной и согласованной в отношении начальной скорости и магнитного состояния. Та
группа, которая движется через дрейфовую трубку с кинетической энергией меньшей, чем 10-6 эв, должна находиться в основном состоянии.Электроны, прошедшие через дрейфовую трубку, детектируются электронным умножителем (рис. 1), выходной сигнал которого, после усиления и анализа величины импульса, служит отсчётом каждого детектированного электрона. Число электронов, пришедших в каждом 2,5 мсек интервале после прекращения импульсной эмиссии из катода, фиксируется в запоминающем устройстве 400-канального счётчика. Каждый импульс содержит около 109 электронов, но в лучшем случае лишь один с энергией ниже 10–9 эв. После накопления времён пролёта электронов порядка 10000 импульсов анализируется распределение времени пролёта для определения потенциала в дрейфовой трубке, как описывается ниже.
Если бы в трубке не было других полей, кроме гравитационного, и все электроны покидали катод в одно и то же время, ни один из них не достигал бы детектора после tmax=(2h/gf)1/2, где h — длина дрейфовой трубки и gf — ускорение свободно падающего электрона. Однако действие тяжести на частицы в металлических стенках дрейфовой трубки вызывает однородное электрическое поле, величина которого, по расчёту Шиффа и Барнхилла [12], равна Ew=mg/e и направлена так, что оно точно уравновешивает вес электронов и gf=g, где
g — гравитационное ускорение макроскопической материи. Мы нашли целесообразным наложить дополнительное слабое однородное электрическое поле Еа с помощью постоянного тока в дрейфовой трубке параллельно её оси. Учитывая эти поля, максимальное наблюдаемое время пролёта получаетсяtmax=[2hm/(mgf - еЕw+еЕa)]1/2. (1)
При измерении
tmax для отдельных значений Еa можно контролировать как массу т исследуемых частиц, так и величину mgf – еЕw.В экспериментально наблюдаемых распределениях времён пролёта число отсчётов на канал уменьшается до постоянной основной величины с увеличением времени пролёта. Время пролёта, при котором распределение получается постоянным, принимается за
tmax. Визуальное исследование распределений, получаемых при различных значениях Еa, показывает, что tmax обратно пропорционально Еa1/2. Кроме того, эта зависимость соответствует электронной массе частиц. Например, при наложении поля в 5·10–11 в/м видно, исходя из распределения, что tmax равно примерно 0,370 сек, тогда как при поле в 1,3·10–10 в/м величина tmax визуально оканчивается около 0,200 сек. Вставляя эти визуальные оценки в уравнение (1), получаем около 10–11 в/м для Еw – mg/e, что меньше, чем 0,3 mg/e и 5·10–31 кг для m. Это свидетельствует о том, что частица является электроном. В большинстве экспериментов эффект от наложения поля частично затемняется статическими флуктуациями числа отсчётов на канал и счётом постоянного фона; это делает желательным анализ с помощью электронно-вычислительной машины. Кроме того, на распределения влияют задержка и последовательное освобождение электронов вблизи катода и окантовка электрического поля вблизи концов дрейфовой трубки. Для учёта всех этих эффектов нужно связывать полное распределение времён пролёта при полях, имеющих место в дрейфовой трубке, с распределением энергии электронов источника при учёте фона. Пусть ε — минимальная кинетическая энергия электрона, прошедшего дрейфовую трубку. Пусть N(ε) означает число электронов, испущенных катодом с энергиями в интервале 0 — ε. N(ε) пропорционально ε в узком диапазоне энергии электронов, время пролёта которых измерялось. Если эти электроны до входа в дрейфовую трубку — тепловые, то можно показать [11], что распределение, отмеченное у детектора, должно быть пропорциональным ε1/2. При анализе наших результатов мы полагаем N(ε)=Сεγ, где γ определялось экспериментальными распределениями. Пусть t — время прихода электрона к детектору и te — время входа в дрейфовую трубку. Из интеграла энергии имеем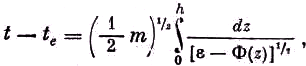 (2)
(2)
где Ф
(z) включает все линейные члены потенциальной энергии, так же как и потенциал окантовки.Последний был аппроксимирован в большей части дрейфовой трубки линейным членом (
mgf - еЕw+еЕa)z≡Fz, а в зоне максимального потенциала (минимума скорости электрона) — квадратичным членом от z, коэффициенты которого были вычислены так, чтобы кривизна Ф(z) соответствовала кривизне, вычисленной по известным потенциалам окантовки. Вычисление t–te для нескольких значений ε οозволило инвертировать интеграл энергии для определения ε как функции от t–te, (mgf - еЕw+еЕa) и т.Мы нашли опытным путём, что максимальное число медленных электронов получается при “смещении” (положительное напряжение относительно дрейфовой трубки) вблизи катода. Поэтому мы должны предполагать, что некоторые, если не все, из наших очень медленных электронов израсходовали дополнительное время в этой ловушке до прохождения дрейфовой трубки, результатом чего является
te. Отсутствие влияния ловушки может встречаться при столкновениях с многочисленными частицами, с другими электронами и остаточным газом или как результаты флуктуаций напряжения в электродах вблизи ловушки. Так как времена прихода подчиняются закону сохранения энергии, мы считаем, что число электронов, входящих в дрейфовую трубку к моменту te, изменяется пропорционально te–η. Поскольку измеряется лишь t, то мы должны определять распределение времён сверх различных времён входа, исходя из Т как ненулевой минимальной оценки te. Тогда число электронов, приходящих после времени t, будет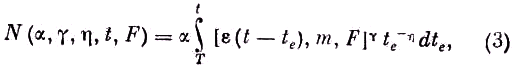
где α — эмпирическая постоянная, пропорциональная общему числу наблюдённых электронов. Число отсчётов в данном временнóм интервале Δ
t будет ΔN/Δt+β, где β — фоновый шум за интервал.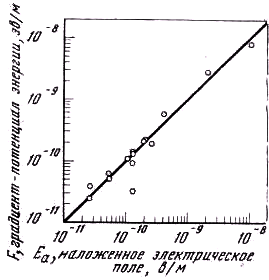
Рис. 2. Экспериментальные измерения градиента потенциальной энергии F в зависимости от наложенного электрического поля Еа
Сплошная линия представляет F=eЕa для частицы, имеющей инертную массу электрона
Была сделана обработка
ΔN/Δt+β по методу наименьших квадратов для каждой серии данных для каждого значения Еa, используя Е, α, β, γ и η как регулируемые параметры. Это было сделано на цифровой вычислительной машине IBM7090 с помощью программы нелинейного выравнивания методом наименьших квадратов [13]. Оптимизированные вычислительной машиной значения F показаны на рис. 2 как функция от наложенного поля. Из рисунка ясно, что mgf - еЕw должно быть весьма малым. Усреднение F–eЕa по 11 сериям экспериментов при Еa<2,5·10–10 в/м даёт 0,13·10–11 эв/м для mgf - еЕw со средним квадратичным отклонением 0,47·10–11 эв/м.Учитывая неточности h, измерений времён полёта, измерений наложенного поля, мы получаем общее отклонение 0,51·10–11 эв/м или около 0,09 mg.
Эксперимент показал, что вертикальная составляющая силы, действующей на электрон, падающий вдоль оси вертикальной медной трубки диаметром 5 см, меньше 0,09
mg. Этот результат согласуется с теоретическим вычислением Шиффа и Барнхилла [12]. Мы заключаем, что сила тяжести электрона в металле та же, что и электрона в вакууме.ЛИТЕРАТУРА
1. R. V. Eotvos, D. Pekar, E. Fekete. Ann. Physik, 1922, 68, 11.
2. P. G. Roll, R. Krotkov, R. H.Dicke. Ann. Phys. (N. Y.), 1964, 26, 442.
3. J. W. Т. Dabbs, J. A. Harvey, D. Paya, H. Horstmann. Phys. Rev., 1965, 139, B756.
4. R. V. Pound, J. L. Snider. Phys. Rev., 1965, 140, B788.
5. P. Morrison, T. Gold. Essays on gravity. Gravitation Research Foundation. New Boston, New Hampshire, 1957, p. 45.
6. P. Morrison. Am. J. Phys., 1958, 26, 358.
7. L. I. Schiff. Proc. Nat. Acad. Sci. U. S., 1959, 45, 69.
8. M. L. Good. Phys. Rev., 1961, 121, 311.
9. W. M. Fairhank, F. С. Witteborn, L. V. Knight. Science, 1964, 144, 562.
10. F. С. Witteborn, L. V. Knight, W. M. Fairbank. Proceedings of the Ninth International Conference on Low Temperature Physics, edited by J. G. Daunt, D. O. Edwards, F. J. Milford, M. Jakub. Plenum Press, New York, 1965, p. 1248.
11. F. С. Witteborn. Thesis, Stanford University, 1965 (unpublished).
12. L. I. Schiff and M. V. Barnhill. Phys. Rev., 1966, 151, 1067.
13. D. W. Marquardt. SHARE. Program Library, Program N NLIN 2, SDA N 3094—01 (unpublished), available from Program Information Department, IBM Corporation, Hawthorne, New York.
Дата установки: 16.
02.2009