[вернуться к содержанию сайта]
На поставленный в заголовке вопрос любой ответит утвердительно. Иначе чем кусок железа притягивается к магниту, чем стрелка компаса поворачивается на север? Магнитное поле (МП) всесторонне изучено экспериментально, строго описано теоретически, а критерием истинности представлений о нём служит практика. МП вращает роторы электродвигателей, генерирует ток на электростанциях, служит рабочей средой в электромагнитах, трансформаторах, ускорителях заряженных частиц и многих других устройствах современной техники. Этим полем закаляют сталь, устраняют усадочные раковины при выплавке металлов, уничтожают накипь в паровых котлах и трубах теплоснабжения, а также парафиновые отложения в нефтепроводах. Магнитная обработка картофеля, семян растений, автомобильного топлива, простой воды и т.д. приводит к фантастическим результатам, не объяснимым современной наукой.
“Магнетические” явления, как и в средние века, окружены туманом таинственности и соседствуют с магическими. Этим пользуются лжеученые, мошенники и шарлатаны. Если средневековые знахари лечили магнитом порчу и сглаз, то ряд ведущих институтов страны продают магнитотерапевтические аппараты, якобы излечивающие сотни болезней самой разной природы. Астрологи “научно” подкрепляют истинность своих предсказаний воздействием космического МП планет. Не обходятся без МП и многочисленные изобретатели вечных двигателей, обещающие неограниченные потоки бесплатной и экологически чистой энергии. Вращением магнита создают мифическое торсионное поле, которым обрабатывают настои трав, получая чудодейственные лекарства от различных болезней. Изобретены магниты, защищающие доверчивых людей от шаровых молний. Магнетизмом объясняют прилипание тарелок к человеческому телу и многие другие непонятные явления.
МП мы ощущаем руками, поднося кусок железа к магниту, а его структуру можем увидеть глазами, воспользовавшись железными опилками. Поскольку МП дано нам в ощущениях, измеряется приборами и используется на практике, оно признано особым видом материи. Ему приписали массу и энергию.
Однако далеко не всё то, что дано нам в ощущениях, является объективной реальностью, то есть материей. Человек обладает богатым воображением и часто чувствует то, чего нет на самом деле. Вспомним “чистую” и “нечистую” силы, леших, барабашек, снежного человека, лох-несское чудовище, НЛО. Ведь все это кто-то видел, слышал, трогал руками, зафиксировал на фотографиях и в протоколах, а на тарелках инопланетян некоторые даже летали. Учёные тоже часто наблюдают несуществующее — квантование напряжения и температуры, холодный ядерный синтез, многие элементарные частицы, торсионное поле и т.д. Вспомним также историю с флогистоном, учение о котором было господствующим в термодинамике времён Ломоносова. Перетекание этой “огненной материи” от горячей печки хорошо ощущается поднесённой к ней рукой. Теория флогистона давала точное описание тепловых явлений и подтверждалась практикой. Несмотря на это, с развитием науки от флогистона пришлось отказаться. При этом понимание тепловых процессов стало более строгим, глубоким и простым.
А не таким ли “флогистоном” является и МП, понятие о котором досталось нам из истории? В самом деле, что это за материя, которая исчезает при переходе от неподвижной системы отсчёта к движущейся вместе с зарядом? Что за поле, если оно не имеет своих материальных носителей — магнитных зарядов, монополей (даже у элементарных частиц магнетизм обусловлен круговыми токами)? Может ли материальное МП заставить двигаться носители заряда во вторичной обмотке трансформатора, если на них непосредственно не действует, оставаясь локализованным в железном сердечнике? Возможно ли с материалистических позиций объяснить этим полем отклонение заряженной частицы, пролетающей мимо магнита, вне его МП (эффект Ааронова-Бома)? Таких вопросов, как будет показано ниже, можно задавать множество. Классическая электродинамика Ампера-Фарадея-Максвелла не даёт на них ответа. Основываясь на существовании МП, электродинамика часто противоречит логике и фундаментальным законам природы.
В настоящей работе будет показано, что МП не существует в природе, оно является нашим вымыслом. Все явления и эффекты, приписываемые магнетизму, имеют чисто электрическую природу и без МП описываются более строго, просто и ясно.
По существующим представлениям МП проявляется и фиксируется в двух группах явлений: стационарное — в силовых эффектах взаимодействия движущихся зарядов, переменное — в появлении ЭДС в замкнутом контуре. Эти эффекты будут рассмотрены, соответственно, в первой и второй частях работы.
Термин стационарный, то есть постоянный во времени, создаёт иллюзию чего-то неизменного и неподвижного. Однако стационарное МП — это принципиально динамическое явление. Оно создаётся только движущимися зарядами и обнаруживается только ими.
Считается, что стационарное МП имеется у пролетающих мимо нас электрических зарядов, вокруг пучков заряженных частиц и проводов с током, внутри соленоидов, у полюсов постоянных магнитов. Во всех этих случаях его источником являются движущиеся заряды (в постоянных магнитах из ферромагнетиков имеются молекулярные кольцевые токи, а в магнитах из сверхпроводников — кольцевые макротоки). Даже у элементарных частиц— электронов, протонов, нейтронов МП обусловлено круговым движением заряженной материи.
Доказательством реальности стационарного МП служат силы, действующие с его стороны на движущиеся электрические заряды. Его регистрируют и измеряют по отклонению пролетающих заряженных частиц, по притяжению или отталкиванию проводов с током, магнитов, соленоидов, по повороту магнитной стрелки, намагничиванию вещества и поляризации элементарных частиц. Все эти случаи сводятся к силе взаимодействия двух движущихся зарядов, которую и рассмотрим в первую очередь.
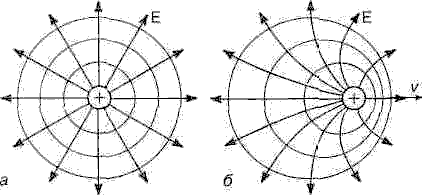
Неподвижный точечный заряд создаёт в окружающем пространстве электрическое поле, напряженность Е которого одинакова во всех направлениях и убывает с расстоянием r как 1/r2. Вектор Е направлен по радиусу, а эквипотенциальные поверхности имеют вид сфер с общим центром на заряде (рис. 1, а). Взаимодействие двух неподвижных зарядов q1, q2 описывается законом Кулона:
F12= F21= q1q2/4πεa2, (1)
где а — расстояние между зарядами, ε — абсолютная диэлектрическая проницаемость среды. При этом силы F12, действующая со стороны первого заряда на второй, и F21 — со стороны второго на первый, равны и противоположны, то есть в соответствии с третьим законом Ньютона действие равно противодействию.

Рис. 1. Структура электрического поля неподвижного (а) и подвижного (б) точечных зарядов.
Окружности — эквипотенциальные поверхностиПоле движущегося заряда отлично от поля неподвижного (рис. 1,б). Эквипотенциальные поверхности уже не являются концентрическими сферами, а их центры смещаются вместе с движущимся зарядом.
Это связано с тем, что поле распространяется с конечной скоростью, равной скорости света, а каждая следующая его порция испускается из новой точки пространства, куда смещается заряд.
Ввиду отличия полей движущегося и неподвижного зарядов сила взаимодействия движущихся зарядов не равна кулоновской Fk (1), а отличается от неё: F=Fk+FМ (сумма здесь векторная). Добавочная сила Fм, возникающая за счёт движения, в классической электродинамике называется магнитной силой и связывается с наличием у движущихся зарядов МП. Она определяется законом Ампера:
F12М= q2[V2В], (2)
F21М= q1[V1В]. (3)
Прямые скобки здесь означают векторное произведение, В1 — магнитная индукция, создаваемая первым зарядом в месте нахождения второго, B2 — вторым на месте первого, V1 и V2 — скорости зарядов.
Если заряды движутся параллельно друг другу, то магнитная сила, как и кулоновская, является центральной и одинаковой на оба заряда, то есть действие равно противодействию. Однако в случае непараллельного движения силы F12М и F21М не равны друг другу и направлены не по одной линии. А если заряды движутся перпендикулярно друг другу, то магнитная сила действует лишь на один из них, без противодействия на второй (рис. 2). Этот результат противоречит одному из фундаментальных законов природы, гласящему, что действие равно противодействию. Выражения для магнитных сил (2, 3) противоречат и другому фундаментальному закону природы — принципу относительности Галилея, так как силы зависят от абсолютных скоростей, а должны определяться относительными. Ампер понимал эти противоречия и давал более сложные выражения для сил, которые в дальнейшем забылись. Разрешая противоречия классической электродинамики, Эйнштейн разработал теорию относительности, введя сокращение размеров, замедление времени и прочее для движущихся тел.
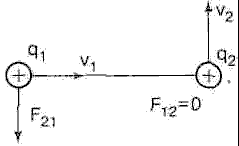
Рис. 2. Магнитное взаимодействие двух движущихся зарядов
q1, q2 по классической электродинамикеВведение магнитных сил в классической электродинамике оказалось необходимым ввиду того, что в ней не учитывается отличие электрического поля движущегося заряда от поля неподвижного, а сила взаимодействия движущихся зарядов рассчитывается по статической формуле Кулона (1). Соответственно электрическое поле движущихся зарядов определяют по статическому уравнению Максвелла divD=ρ (D=εЕ — электрическая индукция, ρ — объёмная плотность заряда). Если бы Эрстед, Ампер, Фарадей, Максвелл и их последователи учли разницу электрических полей, изображенных на рис. 1,а и 1,б, то необходимость введения МП и магнитных сил отпала бы. Продемонстрируем это на примере взаимодействия токов.
Проводник, по которому течёт постоянный электрический ток, является электрически незаряженным, так как число положительных зарядов в нём равно числу отрицательных и сколько зарядов входит с одной стороны, столько и выходит с другой. Однако, несмотря на компенсацию зарядов, ток создаёт в окружающем пространстве электрическое поле. Это связано с тем, что поле движущихся зарядов (в металлах электроны) отлично от поля неподвижных (положительных ионов). Напряжённость поля проводника с током Е = ЕД-ЕС, где ЕД — напряжённость, создаваемая движущимися зарядами, a ЕС — статическими той же плотности.
Электрическое поле цепочки неподвижных зарядов (заряженной нити) из электростатики равно ЕД=τ/(2πεr), где τ — линейная плотность заряда. Вектор ЕС перпендикулярен оси нити и направлен по радиусу r. Если же цепочка зарядов движется со скоростью V, то их поле, как говорят, сносится назад эфирным ветром — оно отстаёт за счёт конечной скорости распространения с (рис. 3). Поэтому его напряжённость
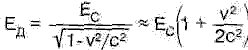 (4)
(4)
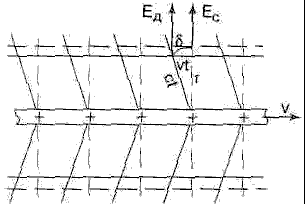
Рис. 3. Электрическое поле движущейся заряженной нити. Пунктиром показана структура статического поля
Приближение справедливо при скоростях V много меньших скорости света с. *)
Суммарное электрическое поле проводника с током
E=V2EC/2c2=μVI/4πr, (5)
где I=Vτ - ток, μ - абсолютная магнитная проницаемость среды. Здесь учтено c2=1/(εμ). Хотя это поле и обнаружено экспериментально (оно особенно сильно вблизи сверхпроводниковых соленоидов, где протекают большие токи), оно не признаётся классической электродинамикой. Для описания же создаваемых им эффектов вводят МП с индукцией
В=μI/2πr. (6)
Однако МП объясняет лишь часть эффектов (например, взаимодействие двух токов) и не может объяснить, например, воздействие постоянного тока на неподвижный заряд, предсказываемое (5).
В 1820 г. Ампер открыл, что два параллельных провода с токами I1 и I2 притягиваются, если токи текут в одном направлении, и отталкиваются, если токи встречные, с силой
F=μI1I2l/2πa, (7)
где а — расстояние между проводами, l — их длина. Он объяснил этот факт взаимодействием магнитных полей токов (6). При этом Ампер не знал о существовании у проводов с током электрических полей (5) и не учитывал силу их взаимодействия. Посмотрим, а не получится ли та же экспериментально измеряемая сила (7) при учёте только электрического взаимодействия проводов, без магнитного. Для определённости свободными носителями заряда будем считать положительные частицы.
Сила взаимодействия двух проводов с токами I1, I2 складывается из четырёх составляющих: отталкивания положительных зарядов первого и положительных второго провода F+1+2, притяжения отрицательных первого и положительных второго F-1+2, притяжения положительных первого и отрицательных второго F+1-2, а также отталкивания отрицательных первого и отрицательных второго F-1-2 (рис. 4) —
F=F+1+2-F-1+2-F+1-2+F-1-2 (8)
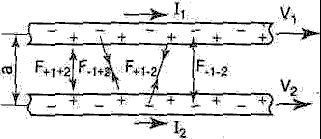
Рис. 4. Силы взаимодействий двух параллельных проводов с токами I1, I2
Последняя составляющая силы между неподвижными отрицательными зарядами определяется из электростатики:
F-1-2= FС=τ1τ2/2πεa, (9)
где τ1, τ2 — линейные плотности зарядов в проводах. Расчёт остальных сил следует вести с учётом движения цепочек зарядов относительно друг друга согласно (4). При этом в соответствии с принципом относительности в качестве скорости V нужно брать относительною скорость, то есть для F+1-2 V1, для F-1+2 V2, а для F+1+2 (V1- V2). В результате после сокращения статических составляющих сил получим
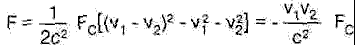 . (10)
. (10)
Подставив сюда значение F по (9), заменив с2 на 1/(εμ), V1τ1 на I1, и V2τ2 на I2, получим выражение Ампера (7). Знак минус означает притяжение. Если один из токов будет обратного направления, то есть отрицательным, то будет сила отталкивания со знаком плюс.
Следовательно, для описания взаимодействия проводов с током не нужно вводить промежуточную среду — МП. Не потеряв, как это сделал Ампер и его последователи, электрическое поле тока, понять и рассчитать это взаимодействие становится проще, строже и нагляднее. При этом отпадают проблемы противоречий с принципом относительности и третьим законом Ньютона.
Наряду с описанными силовыми эффектами стационарное МП проявляет себя в намагничивании вещества. Намагничивание — это приобретение телом магнитного момента рM = qMl, где qM — положительный и отрицательный магнитные заряды, а l — расстояние между ними (рис. 5, а). Магнитный момент единицы объёма вещества М= рM/V, где V — объём тела, называется намагниченностью. Считается, что она пропорциональна напряжённости МП Н:
М=χН (11)
а коэффициент пропорциональности χ называют магнитной восприимчивостью вещества. Чем больше χ, тем лучше намагничивается данное вещество.
На самом деле никаких магнитных зарядов qM, типа изображённых на рис. 5,а у намагниченных тел не существует. Реальны же только круговые токи, представляющие собой векторную сумму круговых молекулярных токов и называемые токами Ампера IA (рис. 5, б). Замена реальной физической картины намагниченного тела (рис. 5,б) на мифический магнитный диполь (рис. 5,а) возможна потому, что на достаточно большом расстоянии от тела МП В этих структур практически одинаково, а именно оно и наблюдается в эксперименте. Различие ближнего МП структур проявляется лишь в специально поставленных экспериментах, в которых, в частности, показано, что элементарные частицы обладают круговыми токами по рис. 5,б, а не магнитными зарядами по рис. 5,а.
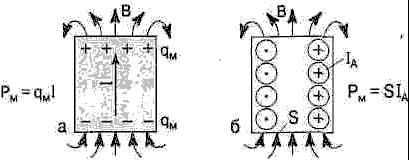
Риc. 5. Структура магнитного дипольного момента рM c магнитными зарядами qM (а) и круговыми электрическими токами Ампера IA (б)
Если площадь основания тела S, а высота l, то в соответствии с рис. 5,а его магнитный момент рM = MSI, а по рис. 5,б рM =SIA. Приравнивая эти значения, получим, что IA=Мl. Если теперь от тока IA перейти к его плотности на единицу длины тела JA= IA/l, то окажется, что
М=JA. (12)
Следовательно, намагниченность М есть не что иное, как линейная плотность кругового тока Ампера.
Известно, что ток не может создаваться стационарным МП, как это утверждает соотношение (11) классической электродинамики. Ток возбуждается только электрическим полем. Причём, для возбуждения кругового тока электрическое поле должно иметь круговую ЭДС E, то есть быть вихревым. Тогда только при неравной нулю круговой проводимости G0 будет ток IA = G0E. В дифференциальной форме это уравнение выглядит так:
JA=γ0rotE (13)
где γ0= G0l/S — удельная круговая электрическая проводимость вещества, имеющая размерность 1/(Ом·м) или См/м.
Из полученного уравнения (13) следует, что для “намагничивания” вещества нужно не МП, а неоднородное, вихревое электрическое поле, ротор которого (то есть dEy/dx-dEх/dy) не равен нулю. Такое поле и создают намагничивающие устройства — соленоиды, магниты.
Круговая проводимость характеризует способность вещества “намагничиваться” (по существующей терминологии), а точнее — проводить круговой электрический ток. В диамагнетиках γ0 мала и отрицательна. В парамагнетиках, где имеются круговые токи неспаренных электронов, ориентируемые вихревым электрическим полем, γ0 положительна. В ферромагнетиках ниже точки Кюри происходит спонтанная ориентация орбит круговых токов неспаренных электронов и ток Ампера возникает сам собой, без внешних воздействий. При этом γ0 оказывается равной бесконечности. Это означает, что ферромагнетики являются сверхпроводниками, но не обычными с бесконечной линейной проводимостью, а круговыми с бесконечно текущим круговым током. Критическая температура ферромагнитных сверхпроводников равна их точке Кюри. Поэтому ферромагнитные вещества являются самыми высокотемпературными сверхпроводниками.
Классические (то есть линейные) сверхпроводники также могут “намагничиваться” вихревым электрическим полем и оставаться постоянными магнитами сколь угодно долго. Однако протекающий в них круговой ток непрерывный, а не складывающийся из множества молекулярных круговых токов, как в ферромагнетиках.
Таким образом, силы магнитного взаимодействия имеют чисто электрическую природу. Они связаны с отличием электрического поля движущихся зарядов от поля неподвижных. Для их понимания и расчёта нет нужды во введении магнитного поля.
“Намагничивание” вещества также связано не с магнитным полем, а с возбуждением круговых токов вихревым электрическим полем. Поэтому ферромагнетики являются высокотемпературными сверхпроводниками по круговым токам.
В первой части настоящей работы* показано, что силовые эффекты магнитного поля (МП) легко объяснимы при учёте электрического поля провода с током или магнита с круговым током Ампера. Учёт не принимавшегося ранее во внимание электрического поля тока при трактовке опытов Эрстеда-Ампера не требует введения стационарного МП и позволяет обойтись без него.
В 1831 г. М. Фарадей обнаружил появление ЭДС в замкнутом контуре (катушке) при включении или выключении тока в рядом расположенной катушке. Поскольку уже при постановке экспериментов он ставил задачу “превратить магнетизм в электричество” (электричество в магнетизм, как считал он, уже превратили Эрстед и Ампер), то возникновение ЭДС, естественно, связал с МП катушки с током, а открытое явление назвал электромагнитной индукцией. Согласно закону электромагнитной индукции Фарадея в замкнутом контуре площадью S МП с индукцией В индуцирует ЭДС, равную скорости изменения магнитного потока BS через этот контур: E= -d(BS)/dt. Знак минус означает, что возникающая ЭДС препятствует изменению потока (правило Ленца).
Закон Фарадея фактически содержит два разных закона: 1) E=-BdS/dt, когда магнитная индукция стационарна, а меняется площадь контура, 2) E=-SdB/dt, когда контур неподвижен, а переменным является МП. В первом случае ЭДС возникает за счёт силы Лорентца, действующей на носители заряда в движущемся контуре. Она объясняется электрическим взаимодействием движущихся зарядов, рассмотренным в первой части. Во второй части работы речь пойдёт лишь о переменном МП и втором случае закона Фарадея.
В 1872 г. Дж.К. Максвелл обобщил экспериментальные законы электричества, магнетизма и их связи между собой, ввёл дополнительное понятие тока смещения, придя к выводу о существовании электромагнитного поля. Система уравнений Максвелла этого поля завершила формирование классической электродинамики, ставшей теоретической основой современной электро- и радиотехники.
По классической электродинамике единственным доказательством существования переменного МП является появление ЭДС индукции при помещении замкнутого контура в это поле. Рассмотрим, нельзя ли наведение ЭДС объяснить и без МП.
Из уравнений Максвелла вытекает, что в свободном пространстве могут распространяться электромагнитные волны. Такая волна имеет две составляющие — электрическую Е и магнитную В, причём векторы Е и В перпендикулярны друг другу и направлению распространения (рис. 1). Скорость распространения волны равна с=(εμ)-1/2, где ε и μ — абсолютные диэлектрическая и магнитная проницаемости среды. Для свободного пространства (вакуума) ε= ε0= 8,85·10-12 Ф/м (электрическая постоянная), μ= μ0 = 4π·10-7 Гн/м (магнитная постоянная), поэтому с= 3·108 м/с — скорости света. Амплитуды электрического поля, направленного на рис. 1 по оси z, и магнитного — по оси у, связаны между собой соотношением dBy/dt= dEz/dx. Максимумы электрического и магнитного полей в максвелловской волне совпадают. В пучностях полей максимальны и их энергии, тогда как в узлах равны нулю. Это противоречит закону сохранения суммарной энергии, которая должна быть постоянной.
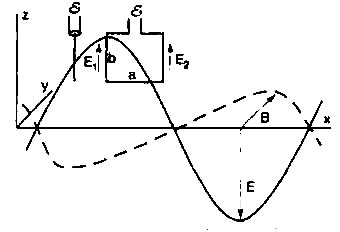
Рис. 1
. Электромагнитная волна в свободном пространстве и измерение её составляющихОписанная структура электромагнитной волны может быть проверена экспериментально. Для измерения электрической составляющей берут зонд в виде штыря длиной b, много меньшей длины волны, и направляют его вдоль оси z — параллельно вектору Е. На штыре появляется ЭДС EЭ= Еb. Для регистрации магнитной составляющей В берут контур, например, рамку размерами а×b, много меньшими длины волны, и устанавливают его перпендикулярно вектору В (рис. 1). По закону Фарадея в рамке индуцируется магнитная ЭДС
E
M = -ab dBy/dt, (1)или с учётом приведённого выше соотношения между Е и В
E
M = -ab dEz/dx. (2)Эксперимент подтверждает формулы (1, 2), что считается подтверждением представлений классической электродинамики об электромагнитных волнах.
Однако выше не было учтено наведение ЭДС в боковых стенках рамки электрическим полем волны, которая равна
E
Э = Е1b-Е2b = -ab dEz/dx (3)(Е1 и Е2 — напряжённости поля у левой и правой сторон рамки).
“Электрическая” ЭДС (3) оказывается в точности равной “магнитной” (2). При наличии обеих составляющих эксперимент должен давать удвоенное значение ЭДС, однако реально измеряется лишь одно — (2) или (3). Следовательно, одного из них не существует. Так как электрическая волна есть заведомо (она регистрируется электрическим зондом), то волны магнитной нет. Нет и переменного МП в свободном пространстве.
При протекании стационарного тока провод электрически нейтрален, так как входной ток на любом его отрезке равен выходному, и заряды не накапливаются. Классическая электродинамика принимает провод нейтральным и при протекании по нему переменного тока в условиях квазистационарности. Но тогда возникают проблемы с объяснением ЭДС, появляющейся в контуре, расположенном вблизи провода (рис. 2). Для выхода из положения полагают, что вокруг провода существует МП с той самой индукцией, что и у постоянного тока (формула (6) первой части). Вот это МП якобы и создаёт ЭДС в контуре по закону электромагнитной индукции Фарадея:
E
M = ab dB/dt=(μab/2πr)di/dt (4)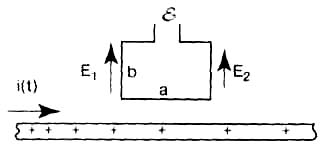
Рис. 2. Поле провода с переменным током и контур для его измерения
На самом деле, провод с переменным током всегда заряжен, так как в фиксированный момент времени t в его произвольное сечение с координатой х втекает ток i(t), а из сечения х+Δх вытекает i(t-Δt), не равный i(t). Здесь Δt= Δх/с — время распространения тока на участке Δх. На отрезке Δх существует заряд Δq = i(t)Δx/c. Линейная плотность заряда
τ= Δ
q/Δx=i(t- х/с)/с. (5)Заряженный провод создает в окружающем пространстве радиальное электрическое поле, напряжённость которого согласно электростатике
E= τ/2πεr=i/2πεcr. (6)
Это поле наводит в контуре ЭДС электрической природы, так как значения Е1, Е2 напряжённости на левой и правой боковых сторонах рамки (см. рис. 2) не одинаковы:
E
Э = Е1b-Е2b = ab dE/dx=(ab/2πεc)di/dx. (7)Учитывая, что di/dx= (1/c)(di/dt), а с2= 1/(εμ), это выражение полностью совпадает с известным (4), полученным по МП. Эксперимент не даёт удвоенного значения ЭДС EЭ+ EМ, поэтому одной из её составляющих реально не существует. В наличии электрической компоненты ЭДС легко убедиться с помощью электрического зонда — штыря, перпендикулярного проводу. Значит, отсутствует магнитная ЭДС (4), а следовательно, и само МП провода. Заряды провода с переменным током действуют на носители заряда в контуре непосредственно своим электрическим полем, а не через посредство искусственно вводимого МП.
Одним из ярких проявлений МП считается явление самоиндукции, на котором основана работа катушек индуктивности — важнейших деталей электро- и радиоаппаратуры.
Опыт показывает, что на участке цепи с нулевым активным сопротивлением при протекании переменного тока i(t) падает напряжение
u(t)= Ldi/dt. (8)
Величина L называется индуктивностью участка цепи.
Откуда же взялась разность потенциалов и на участке цепи, если его сопротивление равно нулю? Чтобы ответить на этот вопрос, в классической электродинамике были вынуждены ввести ЭДС самоиндукции, противодействующую изменению тока и равную напряжению и (8) с обратным знаком. Такое искусственное введение в цепь ЭДС усложняет и запутывает понимание вопроса.
На самом деле, через любую цепь электрический ток проходит конечное время ввиду того, что скорость его распространения не бесконечна. Поэтому сигнал задерживается в цепи на некоторое время tЗ. Если потенциал и ток на входе цепи равны φ(t) и i(t), то на выходе — φ(t-tЗ) и i(t-tЗ) (рис. 3). Отсюда разность потенциалов на участке цепи (или падение напряжения) u= φ(t-tЗ)-φ(t)≈tЗdφ/dt. Здесь учтено условие квазистационарности для рассматриваемой цепи, согласно которому время задержки tЗ много меньше времени изменения тока. Так как φ= Z0i, где Z0 — волновое или характеристическое сопротивление цепи, то
u= Z0tЗdi/dt (9)
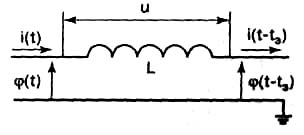
Рис. 3. Катушка индуктивности как линия задержки
Полученное выражение (9) совпадает с экспериментальным (8) при условии, что индуктивность
L= Z0tЗ. (10)
Так как Z0 пропорционально (μ/ε)1/2, a tЗ - l(εμ)1/2, то индуктивность по (10) прямо пропорциональна магнитной проницаемости среды μ и длине цепи l. Этот вывод, а также результаты расчёта индуктивностей различных линий совпадают с известными данными, полученными из магнитных представлений.
В многовитковых катушках индуктивности существует ёмкостная электрическая связь между тесно расположенными витками, увеличивающая задержку тока. На каждом витке n-витковой катушки к собственному падению напряжения u1 добавляется индуцированное остальными (n-1) витками. В результате на одном витке падает напряжение nu1 а на всей катушке n2u1. Поэтому индуктивность катушки пропорциональна квадрату числе витков.
Катушки индуктивности используют в качестве так называемых “магнитных” накопителей энергии. При этом считается, что катушкой после отключения источника питания отдаётся во внешние цепи энергия, накопленная ранее в её МП. На самом деле, после отключения источника происходит разряд накопленного в катушке электрического заряда и продолжает проходить ток запаздывания. В самом деле, пусть до момента времени t= 0 через катушку протекал ток I, а затем источник отключили. Тогда ещё некоторое время tЗ после отключения из катушки будет вытекать накопленный заряд, создавая на нагрузке спадающий до нуля ток i(t) и напряжение u(t). При этом выделится энергия тока запаздывания
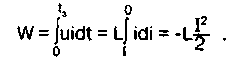 (11)
(11)
Здесь вместо u использовано его выражение (8). Из (11) видно, что никакого отношения к МП энергия катушки не имеет. Катушка индуктивности — это просто линия задержки тока.
Закон электромагнитной индукции был открыт Фарадеем во время экспериментов с двумя расположенными рядом катушками, в одной из которых менялся электрический ток, а в другой регистрировалась ЭДС, то есть фактически с трансформатором. В современных, трансформаторах кроме первичной и вторичной обмоток 1, 2 обычно имеется ещё железный сердечник 3, объединяющий их (рис. 4). По мнению Фарадея и его последователей, явление возникновения ЭДС во вторичной обмотке при изменении тока в первичной (взаимная индукция) объясняется тем, что ток i1(t) создаёт поток магнитной индукции B1(t), который, пересекая вторичную обмотку, индуцирует в ней ЭДС
E
2= Mdi1/dt, (12)где М — взаимная индуктивность обмоток.
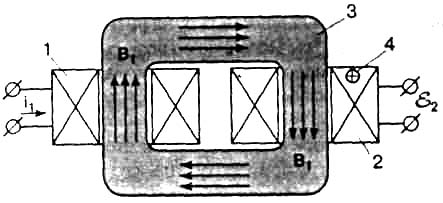
Рис. 4. Трансформатор с железным сердечником
В этом объяснении кроется противоречие. В самом деле, считается, что ток во вторичной обмотке создаётся МП первичной. Однако магнитный поток сосредоточен в железном сердечнике, а вне сердечника МП нет (поля рассеяния не в счёт — они только ухудшают работу трансформатора). Поэтому на носители заряда 4 (см. рис. 4) в проводах вторичной обмотки никакое МП не действует и заставить их двигаться, то есть возбудить ток i2, не может. Природа взаимной индукции в чём-то другом.
Аналогичные трудности в классической электродинамике возникли при объяснении эффекта Ааронова-Бома: заряженные частицы, пролетающие мимо МП и не пересекающие его, изменяют свою траекторию. Следовательно, прямое силовое воздействие МП на частицу отсутствует, а она отклоняется. Для объяснения такого парадокса теоретики привлекли квантовую механику, согласно которой поведение частицы описывается волновой функцией. Эта функция не локализована в пределах частицы, а имеет длинный “хвост”, который якобы и взаимодействует с МП, заставляя частицу поворачивать. Искусственность такой трактовки эффекта очевидна.
На самом деле, работа трансформатора и объяснение эффекта Ааронова-Бома основаны на электрическом поле тока или магнита, не учитываемом классической электродинамикой. Как показано выше, провод с переменным током заряжен и создает в окружающем пространстве электрическое поле. Это поле и действует на заряженные частицы, заставляя их двигаться или изменять свою траекторию.
На рис. 5 показана упрощённая схема трансформатора, где наружный виток изображает первичную, а внутренний — вторичную обмотки. При подаче тока i1(t) в первичной обмотке создаётся некоторый распределённый заряд, меняющийся со временем. За счёт электрической индукции (ёмкостной связи) такой же заряд обратного знака возникает на проводе вторичной обмотки. Этот заряд создаёт продольное электрическое поле, суммирование которого по вторичной обмотке и даст ЭДС E2 или напряжение u2 на её выходе.
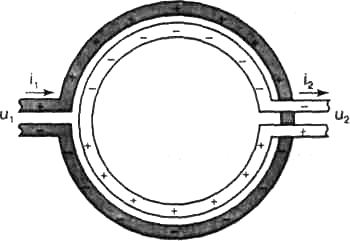
Рис. 5. Упрощённая схема трансформатора
Значение E2, вычисленное по электрическому полю, в точности совпадает с найденным по магнитному потоку (12). Выше это показано на примере длинного прямого провода (первичная обмотка) и прямоугольной рамки вблизи него (вторичная обмотка). В этом можно легко убедиться также на примере идеального трансформатора. Если на его первичную обмотку подано напряжение u1(t), то в условиях квазистационарности оно распределится вдоль провода по линейному закону и на каждый виток будет приходиться напряжение u1/n1 (n1 — число витков). Ввиду плотного прилегания вторичной обмотки на каждом её витке, как на второй обкладке конденсатора, индуцируется то же напряжение u1/n1. На всей же разомкнутой вторичной обмотке, содержащей n2 витков, будет напряжение (или ЭДС)
u2=u1n2/n1. (13)
В случае короткозамкнутой вторичной обмотки (u2= 0) в ней индуцируется ток i2, который полностью компенсирует электрическое поле тока i1. Это произойдёт, если общий ток всех витков вторичной обмотки n2i2 равен общему току первичной n1i1. Отсюда
i2= i1n1/n2. (14)
Таким образом получаем основные соотношения для идеального трансформатора (13, 14) без привлечения понятий магнитного потока и МП.
В трансформаторе с железным сердечником типа изображённого на рис. 4 ток i1(t) создаёт аналогичный круговой ток Ампера в сердечнике (см. первую часть статьи), который своим электрическим полем и воздействует на носители заряда 4 вторичной обмотки. Следовательно, роль сердечника сводится к сближению токов, усилению электрического взаимодействия обмоток и созданию условий идеального трансформатора.
При выводе уравнений электромагнитного поля Максвелл кроме известного тока, обусловленного упорядоченным движением носителей заряда, ввёл ток смещения, связанный с изменением электрического поля. Введение понятия тока смещения считается гениальной догадкой и главнейшей заслугой Максвелла, так как благодаря ему из экспериментальных законов получается волновое уравнение электромагнитного поля.
Единственное проявление тока смещения заключается в создании им переменного МП, а обнаруживается последнее только по ЭДС индукции. Рассмотрим подобный опыт на примере круглого плоского конденсатора (рис. 6).
По Максвеллу переменный электрический ток между обкладками конденсатора не прерывается, а из тока проводимрсти iпр переходит в ток смещения iсм, плотность которого равна dD/dt (D — электрическая индукция или смещение в зазоре). Этот ток создаёт между обкладками круговое МП. Для регистрации МП поместим в зазор контур в виде рамки со сторонами a, b и измеритель ЭДС E. Измеритель должен показать EМ= ab dB/dt.
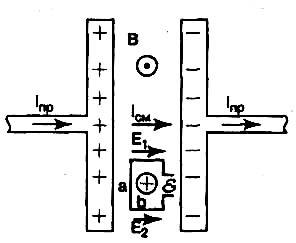
Рис. 6. Конденсатор и общепринятое измерение его тока смещения iсм
по магнитному полю ВКлассическая электродинамика не учитывает неоднородности распределения электрического поля в конденсаторе по его радиусу r, имеющее место даже в условиях квазистационарности (краевые эффекты здесь ни при чём). В круглом конденсаторе это распределение описывается функцией Бесселя. На проводе рамки, находящемся дальше от оси конденсатора, напряжённость поля Е1 меньше, чем на проводе вблизи оси — Е2. Поэтому в рамке должна появиться суммарная ЭДС электрической природы:
E
Э= ab dE/dr. (15)Так как из уравнений Максвелла dE/dr= dB/dt, то ЭДС (15) в точности равна индуцированной магнитным потоком EM. Эксперимент не даёт удвоенного значения ЭДС, поэтому одна из её составляющих лишняя. Наличие электрической составляющей может быть подтверждено измерениями распределения Е по радиусу конденсатора, а само электрическое поле заведомо существует ввиду наличия зарядов на обкладках. Следовательно, не существует магнитной составляющей ЭДС и нет создающего её МП. Значит, опыт не подтверждает наличия тока смещения, а других способов его обнаружения нет. Ток смещения — это абстрактная математическая величина, не имеющая материального носителя, но позволившая Максвеллу из законов электромагнетизма получить волновое уравнение.
Принцип У. Оккама гласит: “Сущности не следует умножать без необходимости”. Как флогистон в термодинамике, так и МП в электродинамике относятся как раз к таким лишним сущностям. Электродинамика без МП станет яснее, строже, точнее, а её изучение и понимание только упростятся.
Все эффекты переменного магнитного поля, как и работа таких “магнитных” устройств, как катушка индуктивности и трансформатор, объяснимы без привлечения МП. Вместо МП нужно всегда учитывать конечность скорости распространения электрического поля и неоднородность его распределения вдоль линии передачи даже в условиях квазистационарности. Конечность же скорости распространения электрического поля, как и любого другого материального объекта, является общим законом природы, не требующим доказательства.
* ЭЛЕКТРО. Электротехника, электроэнергетика, электротехническая промышленность, 2004, № 1.
Дата установки: 20.10.2009
Последнее обновление: 10.11.2009
[вернуться к содержанию сайта]