[вернуться к содержанию сайта]
Для разъяснения различий в мнениях, которые проявились в наших публикациях1, мы заметим следующее.
В частном случае, когда электромагнитный процесс ограничен в конечном объёме, возможно представление процесса как в форме
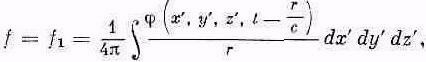
так и в виде

а также в других формах.
В то время как Эйнштейн полагает, что можно ограничиться этим случаем, не ограничивая существенно общности рассмотрения, Ритц считает такое ограничение принципиально недопустимым. Если стать на его точку зрения, то опыт принуждает считать представление с помощью запаздывающих потенциалов единственно возможным, если придерживаться мнения, что необратимость процессов излучения заключена уже в основных законах. Ритц рассматривает ограничение в виде запаздывающих потенциалов как один из источников второго начала термодинамики, тогда как Эйнштейн считает, что необратимость покоится исключительно на вероятностных основах.
Цюрих, апрель 1909 г.
Поступила 13 апреля 1909 г.
* Zum gegenwärtigen Stand des Strahlungsproblems. (Mit. W. Ritz.) Phys. Zs., 1909, 10, 323–324.
1 W. Ritz. Phys. Zs., 1908, 9, 903; A. Einstein. Phys. Zs., 1909, 10,185 (статья 16).
Другой вариант перевода этой статьи Ритца и Эйнштейна, выполненный М. Семиковой, можно найти в приложении к статье Р. Фритциуса на
www.ritz-btr.narod.ru/disagree.html
В последнее время Г. Л. Лоренц1, Джинс2 и Ритц3 выступили в этом журнале с изложением своих взглядов на эту чрезвычайно важную проблему, что облегчает критическое осмысление её современного состояния. Считая полезной дискуссию учёных, серьёзно занимающихся этой проблемой, даже если она и не приведёт к окончательному результату, я хочу сказать следующее.
1. Известные до настоящего времени законы электродинамики проще всего выражаются в форме дифференциальных уравнения Максвелла–Лоренца в частных производных. Уравнения в форме, содержащей функции запаздывающего аргумента, я рассматриваю, в противоположность Ритцу3, только как вспомогательные математические формулы. Меня принуждает к этому прежде всего то обстоятельство, что эти уравнения не включают в себя закон сохранения энергии; в том же, что закон этот выполняется строго, сомневаться, по-моему, не следует, пока не будут найдены веские аргументы для отказа от этого путеводного закона. Правильно, конечно, что уравнения Максвелла для пустого пространства сами по себе не говорят ничего о том, что они изображают лишь промежуточную конструкцию; но точно то же самое, как известно, можно сказать и об уравнениях движения Ньютона, равно как и о всякой теории, которая должна быть дополнена другими теориями, чтобы дать единую картину комплекса явлений. Дифференциальные уравнения Максвелла тем и отличаются от уравнений, содержащих функции запаздывающего аргумента, что в каждое мгновение и во всякой неускоренной системе координат они дают выражение для энергии и количества движения рассматриваемой системы. В теории, оперирующей с функциями запаздывающего аргумента, мгновенное состояние системы вообще нельзя описать, не используя для этого предшествующих состояний. Если, например, источник света А испустил световой сигнал в сторону экрана В, но этот сигнал ещё не достиг экрана В, то согласно теориям, оперирующим с запаздывающими силами, световой сигнал представлялся бы только с помощью явлений, происходивших ранее в излучающем теле при испускании света. Тогда энергию и количество движения — если только вообще не отказываться от этих величин — пришлось бы изображать в виде интегралов по времени.
Но Ритц как раз и утверждает, что опыт принуждает нас отказаться от дифференциальных уравнений и заставляет ввести запаздывающие потенциалы. Однако, на мой взгляд, его доводы нельзя признать убедительными.
Если мы положим вместе с Ритцем

и
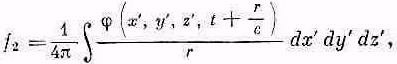
то как f1, так и f2 будут решениями уравнения
(1/c2)∂2f/∂t2–Δf =φ (x, y, z, t),
а значит, и
f3 = a1f1 + a2f2
тоже будет решением при условии а1 + а2 = 1. Однако неверно, что решение f3 является более общим, чем f1 и что, полагая a1 = 1, а2 = 0, мы совершаем переход к частному случаю. Когда полагают
f (x, у, z, t) = f1,
то при этом вычисляют электромагнитное действие в точке х, у, z из тех движений и конфигураций электрических зарядов, которые существовали до момента времени t. Полагая же
f (x, у, z, t) = f2
используют для определения указанного электромагнитного действия такие движения и конфигурации, которые происходят после момента времени t.
* Zum gegenwärtigen Stand des Strahlungsproblems. Phys. Zs., 1909, 10, 185–193.
1 H. A. Lorentz. Phys. Zs., 1908, 9, 562.
2 J. H. Jeans. Phys. Zs., 1908, 9, 853.
3 W. Ritz. Phys. Zs., 1908, 9, 903.
Продолжение статьи можно найти в её полном варианте на
www.ritz-btr.narod.ru/einstein/einstein.html
Дата установки: 28.10.2007
Последнее обновление: 27.09.2012
[вернуться к содержанию сайта]