[вернуться к содержанию сайта]
Как мы теперь знаем, для окончательного разрешения этого парадокса потребовался пересмотр самых фундаментальных представлений о пространстве и времени.
Именно по пути такого пересмотра основ пошёл А. Эйнштейн, создатель специальной теории относительности. В отличие от X. Лоренца, Дж. Фицджеральда, А. Пуанкаре и других, он не ограничивался конкретной целью объяснить отрицательный результат опыта Майкельсона-Морли. Логика его рассуждений была примерно такова. Принцип относительности, сформулированный Галилеем для механических явлений задолго до открытия электромагнетизма, – рассуждал Эйнштейн, – было бы вполне естественно распространить и на электромагнитные явления.
В своей самой первой работе по СТО Эйнштейн приводит такой простой пример: имеется проводник и магнит, которые движутся относительно друг друга с постоянной скоростью. В системе отсчёта, в которой движется магнит, а проводник покоится, согласно законам Максвелла возникает электрическое поле, порождающее в проводнике некоторый ток. В другой системе отсчёта, в которой движется проводник, а магнит покоится, никакого электрического поля вокруг магнита нет, но в проводнике возникает электродвижущая сила из-за сил Лоренца, действующих на движущиеся вместе с проводником свободные заряды. В результате в обеих системах отсчёта текут совершенно одинаковые токи. Таких примеров можно было бы привести множество. Короче, весь опыт указывал на то, что принцип относительности справедлив для всех электромагнитных, а не только механических явлений. Но, как мы уже знаем на примере уравнения для второго закона Ньютона, это должно было бы соответствовать инвариантности уравнений Максвелла относительно преобразований Галилея. Но непосредственная проверка показала, что это не так. Применяя преобразования Галилея к переменным, входящим в уравнения Максвелла, физики убедились, что уравнения Максвелла справедливы лишь в одной выделенной инерциальной системе отсчёта, в той самой системе, относительно которой скорость распространения электромагнитных волн в точности равна постоянной с (в системе, неподвижной относительно “светоносного эфира”). Лоренц нашёл такие преобразования переменных, входящих в уравнения Максвелла, относительно которых уравнения инвариантны. Преобразования эти так и называются “преобразованиями Лоренца”, хотя сам Лоренц придавал им лишь формально математический смысл, физический же смысл этих преобразований оставался нераскрытым.
Таким образом, возникла проблема выбора: либо отказаться от сформулированного выше принципа относительности, либо видоизменить теорию Максвелла, вводя какие-то дополнительные гипотезы о свойствах эфира (абсолютного пространства), либо отказаться от справедливости преобразований Галилея. Последнее означало бы отказ от тех привычных представлений о пространстве и времени, из которых с такой очевидностью следовали преобразования Галилея! Эйнштейн первым понял, что, вопреки “здравому смыслу”, опыт, беспристрастный судья, вынес приговор именно преобразованиям Галилея, а вовсе не принципу относительности или электромагнитной теории Максвелла. Дело в том, что во всех экспериментах, не связанных с попытками обнаружить абсолютное движение, т. е. движение относительно эфира, уравнения Максвелла “работали” превосходно, т. е. прекрасно объясняли и предсказывали результаты всех экспериментов. Поэтому, подвергнув сомнению преобразования Галилея, Эйнштейн обратился к самим основам – к таким вопросам, как одновременность и связь между пространственными отрезками и временными интервалами в различных инерциальных системах отсчёта. При этом на вооружение Эйнштейн принял два постулата, основанных на всей совокупности опытных данных. Вот эти два постулата, которых оказалось вполне достаточно для построения всего величественного здания СТО:
I. Принцип относительности: все физические явления протекают одинаково во всех инерциальных системах отсчёта. Это означает, что говорить об абсолютном движении и об эфире бессмысленно, поскольку не существует эксперимента, с помощью которого можно определить движение наблюдателя относительно эфира.
II. Скорость света одинакова и конечна (а не бесконечна) во всех инерциальных системах отсчёта, не зависит от скорости движения источника и является предельной скоростью распространения какого-либо сигнала.
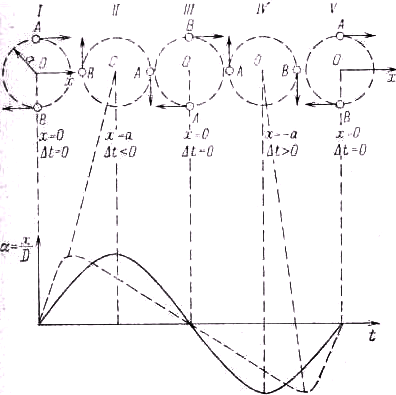
Независимость скорости света от скорости источника противоречит, на первый взгляд, правилу сложения скоростей в ньютоновской механике. Действительно, если источник света движется к наблюдателю со скоростью v и скорость испущенного света относительно источника равна с, то, казалось бы, относительно наблюдателя свет должен двигаться со скоростью с+v. Но многочисленные астрономические наблюдения, в том числе наблюдения двойных звёзд, совершенно определённо опровергали такой ход рассуждений. Если бы для света был справедлив такой простой закон сложения скоростей, то свет, испущенный одной из звёзд в двойной системе, движущейся по направлению к наблюдателю, опережал бы свет, испущенный компонентом, движущимся от наблюдателя (рис. 4). Если учесть это опережение, то видимое взаимное расположение звёзд в двойной системе должно заметно отличаться от той картины, которую давали наблюдения. Следовательно, такого опережения нет, и необходимо отказаться от классического закона сложения скоростей. Раз так, то, казалось бы, необходимо ввести понятие эфира как среды, в которой распространяется свет, подобно тому как звук распространяется в воздухе. Тогда скорость распространения света, так же как и скорость распространения звука, действительно не зависела бы от движения источника, а определялась свойствами среды. Но, если бы такая среда существовала, то наблюдатель, движущийся относительно этой среды (эфира), наблюдал бы, опять-таки в соответствии с классическим законом сложения скоростей, изменение скорости света. Но существование эфира, как мы уже знаем, исключалось опытом Майкельсона-Морли.

Рис. 4. Проверка независимости скорости света от скорости источника по двойным звёздам. Наблюдаемое угловое расстояние α
звезды А от неподвижного центра масс О в двойной системе, состоящей из звёзд A и В и удалённой от Земли на расстояние D (сплошная кривая – синусоида), соответствует независимости скорости света от скорости источника. Если бы был справедлив классический закон сложения скоростей, то получалась бы штриховая кривая, не согласующаяся с наблюдениями, опережающая (Δt > 0) или отстающая (Δt < 0) от синусоиды.Следовательно, астрономические наблюдения двойных звёзд и результат опыта Майкельсона
-Морли вместе взятые противоречили закону сложения скоростей (3.2). Закон же сложения скоростей, принятый в ньютоновской классической кинематике, является непосредственным следствием абсолютности времени, о чём уже говорилось при обсуждении преобразований Галилея (3.1). Теперь ясно, что путь, избранный Эйнштейном, – анализ самых фундаментальных свойств пространства и времени и в первую очередь анализ понятия одновременности – был продиктован всей совокупностью опытных данных.Дата установки: 1
4.04.2007[вернуться к содержанию сайта]