[вернуться к содержанию сайта]
Гн. Эйнштейн придерживается того мнения
(1), что отмеченная мною (2) многозначность интеграла дифференциального уравнения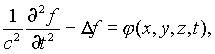
(С = скорости света) несостоятельна, по меньшей мере не в том смысле, что частные интегралы
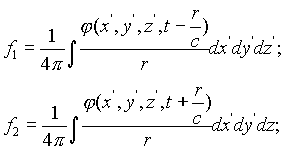
наконец
соответствуют не одним и тем же процессам. Напротив, первый случай указывает на то,
(1) Physikal. Zeitschr., t. X, 1909, p.185.
(2) Œuevres, XVIII, p.493.
c. 504
что поле для
(x, y, z, t) подсчитывают исходя из известных предшествующих состояний, во втором же случае подсчёт ведётся исходя из последующих состояний, так что выбор между
и 
касается способа вычислений, но не сущности процесса. Эта точка зрения совершенно несостоятельна. Если в момент времени t на теле А происходит кратковременный процесс, связанный с излучением, то на электроны тела В, находящегося на большом удалении r, согласно импульс подействует в момент 
; если принять , то такой импульс появится в момент в момент времени 
(прежде чем состоялся процесс на теле А!); согласно же 
для тела В возникают два импульса в моменты времени и . Итак, последний процесс существенно отличается от двух других, и в общих случаях эти два также не перекрывают друг друга при перемене знака времени. Здесь идёт речь не о другом способе вычисления, но о совершено ином процессе.
В случае конечного ограниченного пространства, полагает далее Эйнштейн, процессы могут быть представлены как с помощью
, так и посредством . Однако это не так. Согласно известным положениям к интегралу плотности электричества или электрических токов ( или ) приводит поверхностный интеграл, который не зависит от названных величин. В такой форме можно использовать при вычислении поля как предшествующие, так и последующие значения времени. Однако предположение Лоренца заключается как раз в том, что при использовании и предпосылке большого пространства интеграл по поверхности упраздняется, из чего следует, что он не исчезает в общем случае при использовании для того же самого процесса.
Однако наряду с интегралами
, , существует бесконечное множество других, и является совершенно неприемлемым, изначально и вообще, говорить об излучающих или поглощающих полях, как это делает А.Эйнштейн. Если бы удалось благодаря каким-либо новым предположениям из этого множества решений выделить , и как единственно пригодные к рассмотрению, то нетрудно, направив вектор излучения в бесконечность, представить как единственный интеграл.
c. 505
Речь идёт об очень сложном вопросе, и всё, что до сих пор привлекалось к его решению, следует отклонить как несостоятельное, что обстоятельно рассмотрено мною в другом месте (1).
Гн. Эйнштейн упрекает далее теорию, оперирующую запаздывающими силами, в том, что она может описывать состояние системы (энергия и характеристики движения) лишь обращаясь к предшествующим состояниям таковой, в то время как дифференциальные уравнения в частных производных дают её состояние в любой момент времени. Однако вопрос заключается в том, согласуется или не согласуется это мгновенное состояние с формулами запаздывающих потенциалов. В первом случае одна картина (с запаздывающими потенциалами – В.Ч.) выглядит точно также как и другая (уравнения в частных производных – В.Ч.), хотя в несколько изменённой форме; напротив, во втором случае процесс таков, каким он в действительности
никогда не наблюдался. Если удастся строго во всей всеобщности вывести из уравнений в частных производных при посредстве приемлемых дополнительных гипотез тот факт, что решение, которое позволяет вывести себя не из запаздывающих потенциалов, оказывается ненаблюдаемым, то трудность будет устранена. Напротив, до сих пор я усматриваю в том, что запаздывающие силы являются единственным истинным интегралом уравнений (по отношению к холодному мировому пространству) и что на большом удалении энергия вследствие этого течёт наружу или, по крайней мере, никогда не течёт внутрь, основание необратимости и второго основного закона. Здесь неуместно пояснять, что посредством суррогата картины “эфира” и при помощи определённых энергетических представлений можно отклонить рассмотренные и многие другие трудности.Поэтому я должен решительно подтвердить свой вывод, что до тех пор, пока дозволительно дополнять
каким-либо произвольным интегралом дифференциального уравнения
,
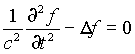согласно методу Джинса-Лоренца необходимым образом будет возникать (даже если отказаться от ограниченного пространства и идеального зеркала) формула излучения, противоречащая
(1) W.Ritz, Œuevres, XVIII, p. 145.
c. 506
опыту. Однако при условии запаздывающих потенциалов этот метод недопустим в силу того, что он оперирует с бесконечным числом электронов (и идеальным зеркалом).
Гёттинген, февраль 1909.
Дата установки: 09.03.2008
[вернуться к содержанию сайта
