[вернуться к содержанию сайта]
с
. 493В сообщении “К теории излучения”, появившемся недавно в этом журнале
(1), Г.А. Лоренц приходит к заключению, что теория “излучения чёрного тела”, развитая Джинсом (2) и им самим (3), несовместима с опытом; поскольку на этом пути вывод формулы излучения может утратить силу. Если внести существенные изменения в основные законы электромагнетизма, то возникает необходимость таких изменений, а именно следовало бы, в духе теории Планка, ввести в теорию нечто подобное атому энергии-времени.Ввиду большой важности этого вопроса и ввиду трудностей, которые, как показал Г.А. Лоренц, сохраняются также и при введении атома Планка, позволительно указать на
(1) Physikal. Zeitschrift, t. IX, 1908, p, 562.
(2) Proc. Roy. Soc., t. LXXVI, 1906, p. 296, 545.
(3) H.-A. Lorentz, Le partage de l’energie etre la matie ponderable etl'ether. Conference tenue au congres de Rome (Roma, Tipografia della R. Accad. dei Lincei), avril 1908.
с
. 494ошибку теории Джинса-Лоренца, непосредственно затрагивающую существенный пункт доказательства, из-за которой оно теряет силу.
Подход к электрическим и магнитным силам, который принят в таком доказательстве, является слишком общим; он противоречит формулам запаздывающих потенциалов, которым должно удовлетворять каждое физически допустимое решение основных уравнений. Лишь это условие (запаздывающие потенциалы - перев.) ведёт к значительному ограничению числа координат свободного эфира, которые Лоренц обозначает как
Как известно, благодаря введению потенциала основные уравнения лоренцевской теории электромагнетизма могут быть приведены к общей форме
(1) 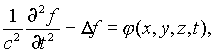
где с = скорости света,
φ обозначает заданную функция от x, y, z, t, и f зануляется на бесконечности. Общее решение этого уравнения, например, по методу Пуассона, содержит в себе две произвольные функции от x,y,z, а именно значения f и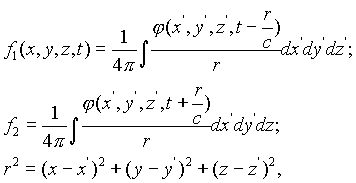
Далее, произвольная линейная комбинация из
f1 и f2с. 495
![]() где
где ![]() ; наконец
; наконец
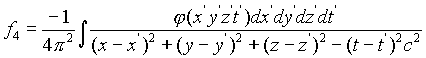 .
.
Решение
f1 соответствует расходящимся волнам, f2 – сходящимся, поступающим из бесконечности, f3 – обоим видам; другие решения опять-таки будут соответствовать волнам, сходящимся или расходящимся по отношению к точке чистого эфира, в которойЧтобы исключить такие невозможные решения, который однако удовлетворяют всем условиям, включая условия в бесконечности, следует прежде всего ввести приемлемое ограничение в произвольно определяемое начальное состояние. Необходимое и достаточное условие, при котором f1 существует для всех для всех значений времени, является такое условие, при котором указанное решение справедливо для времени
с
. 496.Наконец, из характера уравнения (1) как гиперболического дифференциального уравнения вытекает, что, если начальное условие достигнуто весьма приближённо (что здесь можно лишь констатировать), то из этого никак не следует, что формула
f1 справедлива для подобного приближения: могут быть, например, сходящиеся волны, которые в момент времени t0 очень слабы и далеки, но в последующее время в заданной точке пространства могут принять любое конечное значение.Столь же мало способны выдержать строгую критику другие предложенные к настоящему времени дополнительные условия (1); на почве максвелловских представлений не может быть найден переход от обратимых (
reversiblen) дифференциальных уравнений к запаздывающим потенциалам, благодаря которым только и может быть достигнута необратимость в электродинамике. Итак, важно констатировать, что исчерпывающим выражением законов излучения и теории Максвелла-Лоренца в целом являются не дифференциальные уравнения, но элементарные действия, которые получаются введением запаздывающих потенциалов в лоренцевское выражение пондеромоторной силы. В этой форме исчезают электрический и магнитный векторы, которые в принципе не поддаются прямому наблюдению, но играют лишь роль математических вспомогательных функций (2), в то время как положения (Aussagen) теории относятся собственно только к значениям пространства, времени и электрических зарядов.Для вывода формулы излучения Джинс и Лоренц обращаются к представлению об ограниченном зеркальными стенками пустом пространстве параллелепипеда, в котором находится тело К; электрические и магнитные силы внутри этого пространства являются функциями от
x, y, z и разлагаются в ряды Фурье, коэффициенты которых являются функциями времени и играют роль лагранжевых координат, для которых дифференциальные уравнения могут быть выведены на основе принципа Гамильтона. При таком подходе не принимается во внимание важнейшее условие представимости посредством запаздывающих потенциалов;(1
) Об этой и других слабых сторонах теории Максвелла-Лоренца смотри работу.: Recherches critiques sur ľélectrodynamique générale, Œuevres, XVIII, p. 317.(2) Loc. cit., p. 318.
с. 497
между тем, именно это условие, как было показано выше, исключает из начальных состояний как недопустимую бесконечную многозначность состояний эфира, представленную двумя произвольными функциями от xyz и бесконечно многими параметрами. Оно требует в частности, чтобы силы оставались постоянными, если электрические заряды покоятся. Напротив, согласно уравнениям в частных производных это не является необходимым: здесь всегда может быть прибавлено ещё одно решение гомогенного уравнения 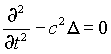 , которое в рассматриваемом случае должно удовлетворять краевым ограничениям на отражающих стенках, и получается тем самым совокупность собственных электрических колебаний пустого пространства (без тела К). Такие решения, как показал Лоренц (loc. cit., p. 14), оказываются допустимыми в выводе Джинса-Лоренца, хотя они не должны иметь места. Более того, бесконечно многие параметры, которые они в себе заключают (коэффициенты разложения общего решения
, которое в рассматриваемом случае должно удовлетворять краевым ограничениям на отражающих стенках, и получается тем самым совокупность собственных электрических колебаний пустого пространства (без тела К). Такие решения, как показал Лоренц (loc. cit., p. 14), оказываются допустимыми в выводе Джинса-Лоренца, хотя они не должны иметь места. Более того, бесконечно многие параметры, которые они в себе заключают (коэффициенты разложения общего решения 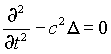 на собственные колебания пустого пространства, т.е. разложения в ряд Фурье), должны оставаться равными нулю. Эти бесконечно многие параметры “чистого эфира” оказываются такими, что согласно положению о равномерном распределении энергии по степеням свободы стремятся поглотить всю энергию и распределить её на самых коротких длинах волн. Таким образом, теория Джинса-Лоренца оказывается недопустимой.
на собственные колебания пустого пространства, т.е. разложения в ряд Фурье), должны оставаться равными нулю. Эти бесконечно многие параметры “чистого эфира” оказываются такими, что согласно положению о равномерном распределении энергии по степеням свободы стремятся поглотить всю энергию и распределить её на самых коротких длинах волн. Таким образом, теория Джинса-Лоренца оказывается недопустимой.
Могут возразить, что рассмотренное решение, разлагаемое на ряды Фурье, может быть интерпретировано как “запаздывающие” силы, порождаемые электронами отражающих стенок. Но так как идеальные отражающие стенки предполагают в себе бесконечное множество электронов проводимости, то по одной только этой причине они должны быть отброшены как недопустимая абстракция, поскольку в действительности число степеней свободы тела К (соответственно, число содержащихся в нём электронов) и число степеней свободы зеркала не могут рассматривать как бесконечно многообразные, и в этом всё дело. Если число электронов зеркала очень велико, то подход Джинса-Лоренца остаётся вообще-то оправданным, но только для собственных колебаний пустого пространства, для которых не принимается во внимание имеющиеся в действительности прерывный (дискретный) характер отражения и конечное числа электронов и проводимости, то есть подход справедлив для длинных волн и низких температур
.с. 498
.Здесь причина того, что указанный подход является правильным для таких и только для таких волн. Напротив, для более коротких волн он никак не совместим с условием запаздывающих потенциалов, он оставляет слишком большое многообразие решений.
Принятие в статистическое рассмотрение условия запаздывающих потенциалов является трудным, и возникает вопрос, является ли оно достаточным, чтобы привести спектральное распределение энергии в соответствие с его экспериментально данным характером. Для этого необходимо определить, сколько и какие именно произвольные константы включает в себя общее решение уравнений движения системы электронов, если в отношении сил используется представление о запаздывающих потенциалах. Только на эти произвольные составляющие может быть распространён статистический подход. В случае механических задач вопрос сильно упрощается тем, что ход процесса определяется заданием координаты q и импульса p. В электронной теории дело обстоит иначе, и в этом, пожалуй, заключается её удивительная особенность. Как показал Герглотц (1), уравнения свободного движения (kräftefreien Bewegung) недеформируемого электрона допускают кроме равномерного перемещения ещё бесконечно много решений. Для очень малой скорости общее решение может быть представлено как сумма бесконечного множества колебаний с произвольными амплитудами, длины волн которых располагаются далеко за пределами известного ультрафиолетового спектра, а именно, имеют в верхнем пределе величину порядка диаметра электрона и не имеют нижней границы. Так как метод Герглотца (2) остаётся применимым также и для общих проблем электронной теории и ведёт к аналогичным интегральным уравнениям, можно в общем случае ожидать решения аналогичного характера. Это обусловлено в конечном счёте тем, что в электронной теории ускорение электрона определено известными предшествующими положениями, скоростями и ускорениями других электронов или заряженных частиц.
(1) G. Herglotz, Gött, Nachr
., 1903, Heft 6; 1904. Heft 8; Math. Ann., t. LXV. 1908, p. 87(2) Loc. cit., 1904.
с. 499
Если ограничиться случаем, при котором все имеющиеся функции вида 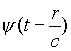 могут быть разложены в соответствии с формулой
могут быть разложены в соответствии с формулой
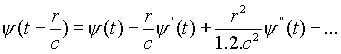
то получаются дифференциальные уравнения бесконечно высокого порядка, общее решение которых зависит от бесконечного множества констант (1), которые, как известно, в этом специальном случае должны удовлетворять условиям сходимости наложенных неравенств. Исследования Зоммерфельда (2) и П. Герца (3) в отношении недеформируемого шарообразного электрона показывают, что при заданной внешней силе ему можно приписать произвольное движение в пределах промежутка времени Т, который равен диаметру электрона, поделённому на скорость света; в частности, при равномерном поверхностном заряде каждая функция с периодом Т удовлетворяет уравнениями движения свободного электрона, и любая подобная функция
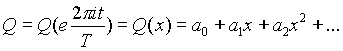
и значения
В общем случае решение для произвольных систем подвижных электронов точно так же может требовать для себя бесконечного множества констант и допускать волновые (
oszillierende) решения с неограниченно малыми длинами волн. Эти решения обусловлены только бесконечно многими “степенями свободы эфира”; и следует опасаться, что в соответствии с предположением о равномерном распределении энергии они могли бы в итоге вновь воспроизвести тенденцию к полной концентрации излучения на коротких волнах,(1) Vgl. T. Lalesco, Sur
ľéquation de Volterra, Thése, Paris, 1908.(2) Gött. Nachr., 1904, p. 363.
(3) Math. Ann., t. LXV, 1908, p. 1.
с. 500
хотя формула приняла бы вид, отклоняющийся от джинсовской. Но даже и без этих соображений должны существовать, например, свободные колебания электрона, которые накладываются на всякое решение и на которые может быть разложено каждое решение, так что они должны обнаруживаться повсюду, хотя экспериментально это представляется невероятным. Если даже такое излучение на чрезвычайно коротких волнах не должно стать доступным нашим методам наблюдения, то должен обнаруживаться соответствующий весьма заметный энергетический дефект, который не был нигде зафиксирован.
Из этого можно заключить, что подобно тому, как мы уже были вынуждены значительно уменьшить многообразие решений уравнений теории Максвелла посредством введения запаздывающих потенциалов, требуется такое же новое ограничение, чтобы привести к конечному значению число определяющих элементов (констант) решений.
Тот факт, что среди бесконечного числа возможных допустимых решений всегда есть одно исключительное, подобно тому как среди решений уравнений в частных производных были выделены запаздывающие потенциалы, может получить простое разъяснение. Думается, что гравитация действует не мгновенно, но в соответствии с электродинамическими законами. Чтобы рассчитать в таком случае движение при заданных начальных значениях координат и скоростей, изначально в качестве первого упрощения исходят из классических законов движения; это решение включают затем в (очень малые) дополнительные члены, которые введены новым законом; так появляются новые дифференциальные уравнения второго порядка, которые интегрируют для тех же самых начальных значений и т.д. В итоге получается решение, в котором каждая координата
x оказывается определённой аналитической функцией времени t и начальных значенийс. 501
для которых этот метод неприемлем ни при каких обстоятельствах (nie), и которые в лучшем случае могли бы соответствовать диковинным планетным системам. В случае свободного электрона получают простое равномерное движение. Если это решение принять как единственно допустимое, то множество произвольных констант, соответственно, многозначность решения, окажется не большим чем в механике, именно, равно удвоенному числу степеней свободы электронов.
Этого можно достичь введением дополнительного условия в форме принципа наименьшего действия, хотя при этом исчезает вариация для всех решений, действительный минимум может проявиться только для одного определённого решения. Подобное имеет место, например, в теории колебаний струн, мембран и т.п. (1), где исчезают вариации для всей совокупности бесконечно числа собственных колебаний, но достигается минимум для основной гармоники. Можно было бы точно так же наряду с условиями в бесконечности ввести условия для очень больших значений
t, которые опять-таки следует отклонить при помощи вариационного исчисления.Принципиальные трудности в теории излучения чёрного тела, отмеченные Лоренцем, ведут нас не столько к тому, чтобы вместе с Планком вводить частицу (
Element) энергии-времени, но гораздо более к требованию восстановить при помощи принципа наименьшего действия нарушенный современной электронной теорией принцип детерминизма (однозначности - Eindeutigkeit) природных процессов в духе классической механики, чтобы известное конечное число заданных факторов было достаточным для определения процесса движения системы электронов в любой момент времени.Вместе с этим из законов природы исчез бы последний остаток того, что однажды было названо эфиром. Раз за разом возникала потребность в опыте, чтобы отрицать у него движение и другие материальные свойства; из более или менее сложного механизма он сам превратился в неизменный носитель электромагнитных явлений. В этой превращённой сфере (
reduzierten Gebiete)(1) Vgl. z.B. Riemann-Weber, Partielle Differentialgleichungen, t. II., p. 284. Braunschweig, 1901.
с. 502
его существование ещё могло себя обнаруживать, но всегда посредством решения уравнений, независимых от материи и, соответственно, от электронов (достаточно уравнения 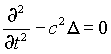 ).
).
Однако опыт вынуждает нас отклонить эти решения. Но в таком случае уравнения электронной теории выражают лишь отношения между пространством и временем, напряжения полей или “состояния эфира” могут быть полностью устранены. Эфир низводится к абстракции: он предстает всего лишь абсолютной координатной системой и математической конструкцией, которая вводит в формулы бесконечное множество констант. Думается, опыт не оставляет ему ни первого ни второго из названных свойств: он полностью изгоняет его из физики.
Для нас при этих условиях рассыпается в ничто (
zerrinnt uns aber in Nichts) важнейшее основание максвелловского описания процессов посредством дифференциальных уравнений в частных производных, которые не обрели физического смысла, но приобрели значение промежуточной математической конструкции, которая сверх того неудовлетворительна для самой себя. Вера в её безусловную достоверность не находит подтверждения тем более, как удаётся показать (1), её всестороннее экспериментальное обоснование с названных сторон полностью отсутствует.(1) W. Ritz, loc.cit.; Œuevres, XIX, p. 427; XX, p. 417; XXI, p. 462.
Дата установки: 09.03.2008
[вернуться к содержанию сайта