[вернуться к содержанию сайта]
Релятивистский принцип относительности сформировался на рубеже ХIХ-ХХ вв. в процессе построения электродинамики движущихся тел. Конечным результатом названного процесса явилась специальная (а затем и общая) теория относительности с её крайне необычной кинематикой, релятивизирующей понятия "пространство" и "время". Ожесточенные споры вокруг новой теории, вызванные релятивизацией указанных понятий, привели в конечном счёте к канонизация теории относительности, критическое отношение к которой стало рассматриваться как признак дурного тона и непрофессионализма.
Однако серьёзные события в науке редко бывают одномерными. С появлением релятивистики теоретическая физика обогатилась ещё одним математическим приёмом - инвариантным преобразованием уравнений Максвелла с помощью группы Лоренца. Но цена, уплаченная не столько за применение, сколько за канонизацию этого приёма, весьма высока. В теоретико-познавательной сфере научное сообщество было вынуждено в явной или неявной форме принять гносеологические основания философского релятивизма и конвенционализма, плохо согласующиеся с методологией экспериментальной науки. В этическом плане утилитаристские соображения пользы возобладали над стремлением к истине, что отразилось и на нравственном климате научного сообщества. Конформизм и соображения научной карьеры во многих случаях стали цениться выше, нежели научное мужество, заставляющее личность отдавать приоритет бескорыстному исканию и защите истины.
Нет сомнения в том, что история релятивистики является драматической страницей науки XX века, отразившей духовные и нравственные надломы и потери века. Однако автор не ставил своей задачей исчерпывающий культурно-исторический анализ этого события в жизни науки. Настоящая работа ограничивается анализом релятивистского принципа относительности в содержательно-гносеологическом аспекте, т.е. в контексте "научная теория - объективная реальность". Свою задачу автор видел в том, чтобы обнажить проблему, решение которой - дело экспериментальной науки.
Суть принципа относительности электродинамики движущихся тел состоит в требовании инвариантности относительно преобразования Лоренца уравнений, выражающих законы физики: "Чтобы специальный принцип относительности мог выполняться, необходимо, чтобы все уравнения физики не изменили своего вида при переходе из одной инерциальной системы в другую, если использовать преобразование Лоренца для подсчёта этого изменения. Говоря на языке математики, все системы уравнений, выражающие законы физики, должны быть ковариантны относительно преобразования Лоренца" [9, с. 101].
Указанное условие принято считать обобщением принципа относительности классической физики, математической формой выражения которого является якобы инвариантность дифференциальных уравнений Ньютона относительно преобразования Галилея. Мы постараемся показать, что принцип относительности Пуанкаре-Лоренца-Эйнштейна является самостоятельным постулатом, применение которого не связано с физической относительностью систем. Более того, как будет далее показано при построении электродинамики движущихся тел релятивистский принцип относительности был использован в ситуации, не удовлетворяющей физическому смыслу относительности.
Принцип относительности классической механики утверждает, что механические процессы в изолированной системе отсчёта протекают независимо от того, покоится эта система или движется равномерно и прямолинейно. И.Ньютон выразил эту закономерность следующим образом: "Относительные движения друг по отношению к другу тел, заключённых в какое-либо пространство, одинаковы, покоится ли это пространство или движется равномерно и прямолинейно, без вращения" [4, с.49].
Принципиальное различие между двумя цитированными высказываниями можно видеть в следующем. В содержание принципа относительности классической механики не входит вопрос о том, как будут соотноситься описания некоторого процесса, полученные один раз в покоящейся, другой раз - в движущейся системе, в то время как вопрос о взаимосвязи указанных уравнений оказывается центральным в релятивистском принципе относительности. Поэтому вопрос о соотношении физического смысла принципа относительности и математического условия инвариантности (ковариантности) "уравнений, выражающих законы физики", приобретает решающее значение для рассмотрения сущности релятивистского принципа относительности.
В общем случае для одного и того же физического процесса можно получить бесчисленное множество описаний, если относить их к разным системам координат, которым приписаны произвольные движения друг относительно друга. В пределах нашей задачи достаточно ограничиться случаем, когда некоторый физический процесс описан в координатах покоящейся системы отсчёта и системы, совершающей равномерное и прямолинейное движение относительно первой. Для наглядности будем считать, что механические процессы, совершающиеся в трюме "корабля Галилея", описываются один раз в координатах, связанных с трюмом корабля, а в другой раз в координатах, связанных с сооружениями неподвижной гавани, из которой ушёл корабль.
Принцип относительности Галилея-Ньютона утверждает, что механические процессы, происходящие в трюме корабля, совершающего равномерное поступательное движение, будут тождественны протеканию этих процессов, когда корабль покоился в гавани. Понятно, что система уравнений, полученных в координатах трюма, не изменится после того как корабль пришёл в равномерное прямолинейное движение, поскольку не изменились как физические условия в системе, так и ход физических процессов. Последнее означает фактически, что принцип относительности Галилея-Ньютона никакой специальной математической формулировки не имеет. Он является качественным принципом, точнее, следствием из закона инерции, которому Ньютон придавал статус одной из фундаментальных аксиом движения. Принцип относительности оказывается как бы "обратной формулировкой"1 этой аксиомы, т.е. закона инерции. Если же мы обращаемся к вопросу о соотношении описаний некоторого явления, полученных в разных системах отсчёта, как этого требует релятивистский принцип относительности, то это уже будет особая самостоятельная задача, которую можно поставить для любых систем отсчёта (инерциальных и неинерциальных, изолированных и неизолированных и т.п.). Обратимся к возникающей в этом случае проблеме.
Уравнения, которыми описываются траектории тел в той или иной координатной системе, могут быть двоякого рода. Иногда бывает достаточно зафиксировать видимую картину движений. В этом случае можно ограничиться уравнениями кинематики, в которые войдут текущие координаты тел, представленные функциями времени. Массы тел, а также все силы и связи, определяющие их траектории, в явном виде в такие уравнения не войдут. Они вообще могут оставаться невыявленными, и при описании видимой картины можно ограничиться уравнениями аналитической геометрии, задающими траектории тел. Например, движение планет солнечной системы в первом приближении описывается уравнениями эллипсов, имеющих соответствующие параметры для каждой из планет. Исторически такое кинематическое описание было шагом на пути к выявлению динамических законов.
Изменение видимой картины движения при смене позиции наблюдателя представляется фактом вполне очевидным. Однако, чтобы это обстоятельство приобрело статус научного факта, потребовалось в своё время его специальное рассмотрение, предпринятое Галилеем. В дискуссии с последователями Аристотеля итальянский учёный должен был объяснить факт вертикального падения ядра к подножию башни, в то время как вращение Земли, на котором настаивал Галилей, защищавший астрономические воззрения Коперника, должно было "относить" ядро в направлении, противоположном этому вращению. Галилей блестяще справился с этой задачей благодаря тому, что ввёл разграничение между относительными движениями тел и общим движением всех тел системы, которое внутри этой системы наблюдать невозможно. Башня и ядро участвуют в совокупном движении, вызванном вращением Земли и её движением по орбите. Но в земных условиях обнаруживается только относительное движение башни и ядра. Наблюдатель вне Земли увидел бы более сложную картину, в том числе и движение ядра по дуге, вызванное вращением Земли.
Эту истину, именно, необходимость отличать относительное движение тел внутри системы от движения самой системы Галилей представил в наглядной иллюстрации с механическими опытами в трюме корабля, который либо покоится в гавани, либо совершает поступательное равномерное движение по тёплой поверхности, надо полагать, Средиземного моря. И в этом случае Галилей подчеркивает различие видимой картины для наблюдателя на корабле и для наблюдателя в гавани. В частности, он указывает, что пишущее перо, колеблющееся в плоскости, перпендикулярной направлению движения корабля, оставит след в виде отрезка прямой на листе бумаги, расположенном на корабле. Но на поверхности воды оно оставляло бы волнистый след (синусоиду). Точно также, подчеркивает итальянский учёный, человек, прогуливающийся по аллее парка в лунную ночь, увидит, что луна скользит над вершинами деревьев и крышами строений в такт движения человека. Но всё это видимая картина, вызванная движением человека, так что, замечает Галилей, нельзя слепо доверять чувственным впечатлениям. Необходимо вмешательство рассудка, дабы отделить видимые (в данном случае - кажущиеся) движения от действительных (реальных) движений тел.
Правила, по которым осуществляется переход от одной видимой картины к другой, достаточно просты. Необходимо всякий раз, как указывает Галилей, к относительным движениям тел системы присовокупить общее движение системы относительно наблюдателя, т.е. геометрически сложить движение наблюдателя и системы тел. В кинематическом плане не имеет значения какой из членов этого соотношения "наблюдатель - система тел" пришёл в движение. Важно, что их относительное движение имеет место и определяет видимую кинематическую картину. Например, наводчик орудия на платформе бронепоезда должен учитывать относительную скорость цели и платформы, на которой установлено орудие. Ему важно их относительное движение и вопрос о том, движется ли взятая в панораму прицела тачанка или движется орудие, отходит на второй план.
Математическим выражением кинематического правила сложения движений, т.е. правила перехода от одной кинематической картины к другой, является преобразование Галилея. Можно встретить точку зрения, навеянную работами Пуанкаре, что преобразование Галилея всего лишь конвенциональный приём (как и преобразование Лоренца). Однако с таким мнением нельзя согласиться. Субъективный произвол при определении реальных пространственно-временных отношений тел не идёт далее выбора единиц измерения, хотя и в этой области он весьма ограничен, поскольку в качестве единиц выбирают в конечном счёте природные эталоны, наилучшим образом удовлетворяющие условиям стабильности, точности и удобства. Что же касается правил сложения координат и скоростей, задаваемых преобразованием Галилея, то они имеют опытное основание в виде операций измерения длин (расстояний) и промежутков времени. Поэтому преобразование Галилея допускает экспериментальную проверку, для осуществления которой достаточно, исходя из галилеева правила сложения скоростей, рассчитать относительные смещения тел, а затем проверить соответствие расчётных величин данным, полученным при проведении соответствующих измерений. Для пущей убедительности можно воспользоваться релятивистским правилом синхронизации часов системы.
Кинематический переход от одной координатной системы к другой со времени Галилея не вызывал никаких затруднений. Однако уравнениями кинематики можно ограничиться только в тех частных случаях, когда движения тел стационарны и не претерпевают изменений со временем. Полную же картину относительных движений дают уравнения динамики, составляемые в той или иной системе. Проблема, поставленная в релятивистском принципе относительности, появляется, как это показала история науки, при составлении динамических уравнений в разных системах. Главный вопрос, который здесь возникает, заключается в следующем. Можно ли удовлетвориться преобразованием Галилея при переходе от покоящейся к движущейся системе отсчёта?
Ответ достаточно очевиден. В одних случаях проблема исчерпывается изменением в движущейся системе кинематических условий, определяемых по правилам Галилея. В других же случаях ограничиться этим нельзя, так как необходимо ввести изменение динамических условий (сил, полей и т.п.) в движущейся системе отсчёта. При этом может оказаться, что наблюдатель движущейся системы будет вынужден воспользоваться при составлении уравнений фиктивными величинами для динамического оправдания видимых движений тел. Иллюстрацию последнего варианта даёт наблюдение тел звёздного неба из вращающегося кресла (вращающейся системы координат) или из ускоренно движущейся ракеты. Вращающийся наблюдатель, связавший с креслом систему координат, припишет громадные линейные скорости и центростремительные ускорения объектам звёздного неба. В соответствии с этим он определит импульсы видимых тел. Эти импульсы также могут принимать огромные значения, но все эти величины окажутся столь же фиктивными, как и те связи, силы (гравитационные поля), которые будет вынужден ввести каш наблюдатель, чтобы решением уравнений динамики, отнесенных к вращающемуся креслу, оправдать видимую картину движений. Фиктивность импульсов, вводимых для объектов небесной сферы, легко обнаруживается тем, что для остановки массивных тел в системе вращающегося наблюдателя потребуется импульс, пропорциональный сумме масс кресла и наблюдатели, но не массам и линейным скоростям небесных тел.
Этот пример показывает, что произвол в выборе системы отсчёта при составлении уравнений динамики крайне ограничен, точнее сказать, этот выбор предопределён реальными физическими связями. Уравнения динамики оправданы физически в тех системах отсчёта, в которых адекватно отражены динамические условия, определяющие движения тел и, тем самым, определяющие видимую картину движения в таких системах отсчёта. Если такие уравнения отнесены к координатам соответствующей системы отсчёта, то они позволяют затем получить видимую картину относительных движений в любой произвольно взятой инерциальной системе координат. На это обстоятельство совершенно справедливо указывал великий Ньютон, различавший видимые (кажущиеся) относительные движения и движения абсолютные, т.е. те, которые возникли вследствие действия соответствующих сил: "Причины происхождения, которыми различаются истинные и кажущиеся движения, суть те силы, которые надо к телам приложить, чтобы произвести эти движения; истинное абсолютное движение не может ни произойти, ни измениться иначе, как от действия сил, приложенных непосредственно к самому движущемуся телу, тогда как относительное движение тела может быть произведено и изменено без приложения сил к этому телу" [4, с.34].
Идеальная система отсчёта, в которой адекватно представлены реальные динамические причины движений, связана с центром масс системы тел. На практике приходится ограничиваться "прикреплением" системы отсчёта к достаточно массивному телу (например, к Земле при расчёте движений в земных условиях). При таком рассмотрении действительных взаимодействий тел становится очевидным, что видимая картина движений, наблюдаемая из вращающегося кресла, возникла вследствие движения кресла в системе массивных тел, а не вследствие сил, приложенных непосредственно к телам небесной сферы. Такие силы, если их захочет ввести вращающийся наблюдатель, останутся "на бумаге". Таким образом, видимые кинематические картины движений могут быть самыми разнообразными в зависимости от позиции наблюдателя, выбирающего координатную систему. Но как только мы переходам к динамическому объяснению и оправданию видимых движений, объективная реальность тотчас же стучится в двери, требуя указания реальных физических связей и сил, выявляемых в соответствующей системе отсчёта.
Приняв во внимание это обстоятельство, можно вновь обратиться к проблеме “динамического перехода” от одной системы к другой. Наиболее простым этот переход оказывается в случае галилеевых инерциальных систем, движущихся в пустоте, так как он может ограничиться применением преобразования Галилея. В этих системах сохраняют свои значения ускорения тел, так как сохраняются значения действующих сил, и уравнения динамики (дифференциальные уравнения Ньютона второго порядка) не изменят своей формы, поскольку в них не входят текущие координаты и скорости тел. В эти уравнения входят, по терминологии Ньютона, лишь приращения абсолютных движений, вызванные действием сил, но не входят приращения движений относительных, обусловленные равномерным движением наблюдателя. Поэтому кинематическую картину в каждой из галилеевых систем можно получить из решения одних и тех же уравнений, описывающих взаимодействие тел, при учёте начальных условий движения в каждой системе. Эти начальные условия в математическом плане представлены постоянными интегрирования. Физически они определяются относительным движением системы и вычисляются согласно преобразованию Галилея. В рассмотренном случае уравнения динамики инвариантны относительно преобразования Галилея.
В тех случаях, когда совершается переход к неинерциалъной системе, удовлетвориться преобразованием Галилея невозможно, так как кроме кинематических условий перехода необходимо учесть изменение в распределении сил, полей и вызываемых ими связей в движущейся системе. В ситуациях, когда системы не изолированные, т.е. движутся в общей для них среде, влияющей на динамические явления, изменение динамической картины при переходе от одной системы к другой вполне очевидно. Менее очевидным оказывается это обстоятельство, когда системы движутся в пустоте, но одна из них негалилеева, т.е. движется ускоренно. Формальный переход к ускоренной системе не вызовет изменения относительных движений рассматриваемых тел. Но эти относительные движения должны теперь вытекать, как уже указывалось, из уравнений динамики, составленных в ускоренной системе отсчёта. И если ускореннее движение системы тел вызвано всего лишь ускорением наблюдателя посредством сил, действующих в покоящейся системе, то наш наблюдатель скорее всего воспользуется фиктивным гравитационным полем, фактически отсутствующем, но введённым в уравнения его системы.
Невозможность в рассматриваемых случаях ограничиться преобразованием Галилея при переходе от одной системы к другой проистекает от того, что эти случаи находятся вне границ физического смысла принципа относительности Галилея-Ньютона. Тем не менее при рассматриваемых переходах можно поставить вопрос о ковариантности (или инвариантности) уравнений движений (уравнений поля) и даже найти группу преобразования координат, обеспечивающую выполнение поставленного условия. Применение подобного преобразования будет сопровождаться по крайней мере двумя условиями. Во-первых, оно возможно в тех случаях, когда динамические условия в движущейся системе однозначно определены её движением относительно покоящейся системы. Примером может служить изменение составляющих напряжённости электрического поля в системе, вызванное её движением в этом поле и косвенно фиксируемое через "утяжеление" заряда (электрона). Во-вторых, преобразование координат, опосредованно выражающее изменение физических величин в движущейся системе, не будет иметь прямого кинематического (пространственно-временного) смысла. Оно играет роль формального приёма, обеспечивающего получение уравнений динамики в той или иной системе, причём решение этих уравнений даёт реальную траекторию частицы (тела), движущегося в поле сил, действие которых на движущееся тело зависит от относительной скорости этого тела (системы отсчёта, связанной с телом) и источника поля (индуктора).

а) системы изолированные, принцип относительности выполняется, задача перехода отсутствует;
б) системы неизолированные, принцип относительности не выполняется, возникает задача перехода: описать в движущейся системе поле покоящейся системы с прямым или косвенным (через преобразование координат) учётом изменения физических условий в движущейся системе.
Рис.1.
Рассмотренная ситуация характерна для электродинамики движущихся тел, поскольку условия перехода от покоящейся системы к движущейся в релятивистской электродинамике не удовлетворяют физическому смыслу принципа относительности. Системы в рассматриваемом случае являются неизолированными, они погружены в общее для них электромагнитное поле, причём одна из систем покоится в этом поле, а другая движется. Преобразование Лоренца найдено для того, чтобы составить взаимосвязанные описания одного и того же поля в покоящейся и движущейся системах координат (рис.1). Для Лоренца отсутствие физической относительности в рассматриваемой ситуации было очевидным, поскольку он руководствовался концепцией эфира, в который погружены системы. Движение относительно эфира должно влиять на электродинамические процессы, и Лоренц хотел найти уравнения поля в движущейся системе, учитывающие указанное влияние. На теоретическую работу Лоренца решительным образом повлиял А.Пуанкаре своим убеждением в том, что электродинамика должна соответствовать принципу относительности, на что наталкивал опыт Майкельсона, справедливый для ситуации "а", рис.1.
Из статей французского математика Г.Лоренц вынес мысль, что удовлетворить принципу относительности значит при формальной тождественности уравнений электродинамического процесса в покоящейся и в движущейся системах (в штрихованных и нештрихованных величинах) найти правило, по которому из уравнений в нештрихованной (покоящейся) системе можно получить точно такие же уравнения в движущейся (штрихованной) системе, применяя переменные соответствующих систем координат. Задачу удалось решить с помощью правила преобразования координат, полученного, можно сказать, путём подстановки. Главный итог применения этого преобразования заключается в приобретении уравнений движения заряда (электрона) в покоящейся системе, удовлетворяющего экспериментам, фиксирующим "утяжеление" заряда.
Уравнение динамики для заряда, движущегося в электромагнитном поле, было найдено опосредованным путём. Благодаря подсказке великого математика Г.А.Лоренц обошёл физическую проблему путём решения своеобразно поставленной математической задачи: добиться в разных системах координат инвариантного описания электромагнитного поля, заданного уравнениями Максвелла в частных производных. Специальная теория относительности отказалась от эфира. Но для ситуации, в которой применяются преобразования Лоренца, использование или не использование эфирной гипотезы роли не играет. А.Эйнштейн не устранил и не мог устранить исходные условия электродинамической задачи, решаемой для систем, погруженных в электромагнитное поле и движущихся друг относительно друга.
Из нашего рассмотрения следует вывод, что лоренц-инвариантность является приёмом математической физики, позволяющим косвенно (через преобразование координат) учесть изменение физических условий в движущейся системе в сравнении с покоящейся системой при получении уравнения движения частицы в поле. С физическим смыслом принципа относительности он “связан” только тем, что применяется для ситуаций, не удовлетворяющих этому смыслу. Вывод преобразования Лоренца из второго постулата СТО ничего не изменяет по существу, поскольку постоянство скорости света является математическим следствием лоренц-инвариантности. А.Эйнштейн, задавшись условием постоянства скорости света, пошёл “от противного”, т.е. от следствия к причине. Этим он лишь ясно обнаружил формально-математический (конвенциональный) смысл второго постулата СТО. Кстати, ни А.Пуанкаре в статье 1895 года, ни А.Эйнштейн в статье 1905 года никакого секрета из этого обстоятельства не делали2.
Новый принцип относительности, формулировка которого приведена в начале статьи, предполагает инвариантное описание в разных системах при условии, что ход явлений зависит от относительного движения систем3. Независимость явлений от движения системы подменена здесь независимостью (инвариантностью) описания явления при переходе от одной системы отсчёта к другой, что позволяет уклониться от рассмотрения физики процессов, обусловленных относительным движением систем4. В рамках общей относительности А.Эйнштейн нашёл группу для ковариантного описания движения тел в инерциальной и ускоренной системах, позволившую и в этом случае обойти вопрос о физической природе гравитационного взаимодействия тел при их быстром относительном движении. Когда А. Логунов утверждает, что "общая теория относительности не является удовлетворительной физической теорией" [3, с. 218], он скорее всего прав. Странным образом он не замечает, что то же самое можно заключить и в отношении специальной теории относительности5, тем более, что если в ОТО не выполняется "закон сохранения энергии-импульса вещества и гравитационного поля", то в специальной теории относительности не выполняется закон сохранения момента количества движения [2, с.219].
Придание статуса физического принципа математическому приёму инвариантного описания можно оценить как драматическое заблуждение теоретической физики XX века. Соблазн математической простоты был настолько силён, что физические соображения оказались на втором плане, и развитие аппарата фундаментальной теории пошло по пути углубления математического формализма. Этим отчасти объясняется увлечение релятивистской кинематикой, повествующей сказочные истории из жизни близнецов. Эти истории никакого физического смысла не имеют, но не могут не вызывать удивление усилия лидеров научного сообщества и средств массовой информации во всём мире, потраченные на провозглашение релятивистской концепции пространства и времени вершиной человеческой мысли.
Последний вопрос касается эксперимента Майкельсона-Морли. Опыт Майкельсона подтвердил в соответствующих пределах точности классический принцип относительности для электромагнитных явлений в изолированных системах. Но релятивистская электродинамика имеет дело с явлениями в неизолированных системах. Поэтому опыт Майкельсона ни подтверждает, ни опровергает релятивистской электродинамики движущихся тел, хотя исторически он сыграл в её становлении парадоксальную роль тем, что укрепил А.Пуанкаре в формально-математическом варианте принципа относительности, который принял из его рук сначала Г. Лоренц, а затем и А.Эйнштейн.
В заключение важно отметить также, что у А.Пуанкаре, выдвинувшего новое понимание принципа относительности, были для этого свои соображения, основанные на позитивистско-конвенционалистской теории познания. Но это уже предмет для другого разговора.
А. Пуанкаре принял активное участие в создании принципа относительности, закрепившегося в релятивистской физике. Новый принцип нельзя свести к оригинальной научно-математической идее. Релятивизм имеет ясно выраженную философскую окраску, которая незамедлительно обнаруживается при попытке совместить формальные предсказания теории (в сфере кинематики) с возможностью наблюдать ожидаемые эффекты. Например, по поводу "сокращения Лоренца" Эйнштейн высказался следующим образом: "Вопрос о том, реально ли лоренцевское сокращение или нет, не имеет смысла. Сокращение не является реальным, поскольку оно не существует для наблюдателя, движущегося вместе с телом: однако оно реально, так как может быть принципиально доказано физическими средствами для наблюдателя, не движущегося вместе с телом" [7, с.187].
Высказывание, сделанное в рамках экспериментальной науки и утверждающее, что вопрос о реальности не имеет смысла, представляется достаточно экстравагантным. Однако указанная позиция не случайность. Органическая связь концепции относительности реальности с релятивистским принципом относительности обусловлена тем, что само появление указанного принципа инициировано, наряду с другими обстоятельствами, философско-гносеологической позицией А. Пуанкаре. Поэтому анализ роли Пуанкаре в возникновении рассматриваемого принципа требует обращения к гносеологической установке учёного.
Философской платформой теоретико-познавательных представлений французского математика является позитивизм, методологические основания которого существенно отличаются от методологии классической науки. Современники и последователи Ньютона в подавляющем большинстве принимали тезис об объективности знания. Философским основанием такой позиции чаще всего был материализм той эпохи, существовавший в рамках концепции деизма (так было у самого Ньютона), либо же вполне последовательный атеистический материализм, снимающий вопрос об идеальных основаниях Бытия, его сотворённости и т.п. Естествоиспытатели рассматривали опыт как контакт с объективной реальностью, в ходе которого опыт рассказывал им на своём языке о том, что происходит в природе. Явления, регистрируемые в опыте, представлялись порождёнными объективными причинами, обнаружившими себя в опыте как проявление сущностных сил природы. Такая позиция была выражена ещё идеологом опытной науки Ф.Бэконом: "Среди названных нами разделов истории особенно важна история искусств, потому что она ... срывает маску и покров с природных явлений, в большинстве своём затемнённых и скрытых за пестротой форм и внешних проявлений" [1, с.223].
Иное отношение к опыту задаётся позитивизмом Э. Маха и А. Пуанкаре. Опытные данные лишаются здесь метафизического смысла и приобретают более субъективную окраску, так как акцент ставится на опыт как на точку встречи внешней реальности и субъекта. Эта "встреча" фиксирована в форме чувственных данных, которые рассматриваются гносеологией позитивизма как самостоятельные ценности вне их связи с так называемыми сущностными силами природы, с объективной реальностью. Чувственные данные предстают как единственная реальность, на которую опирается теория, это уже самоценная реальность опыта. Следствием гносеологии такого рода является отказ от установки на последовательное проникновение вглубь объективной реальности, совершающееся на основе регулятивных принципов объективного характера, на чём настаивал, например, Г. Гегель.
А. Пуанкаре указывает на важное значение фактов опыта, но эти факты он представляет как результат своеобразного "ощупывания" природы человеком, совершающегося вне всякой связи с внутренним содержанием природы. Факты опыта словно отдельные кирпичи, находимые то там, то сям, но эти кирпичи молчат о способе своей выделки. Они суть те простые единицы, которые учёный сам собирает и сам создаёт здание науки из этих кирпичей. Позднее эта идея была выражена Витгенштейном в форме концепции атомарных фактов и атомарных предложений как языковой фиксации опыта. Сам же Пуанкаре следующим образом выражал мысль об опытных фактах как независимых кирпичиках науки: "Факт - всегда факт: студент сделал отчёт по своему термометру, не приняв никаких предосторожностей; пусть так - всё же он сделал отсчёт, и если во внимание принимаются одни только голые факты, то вот перед нами реальность того же ранга, что и странствования короля Иоанна Безземельного" [5, с.92].
Собирание фактов было бы бесцельным и случайным, если бы не направляющее воздействие теории, которая позволяет систематически умножать факты. О соотношении фактов и теории А. Пуанкаре высказался следующим образом: "Я позволю себе сравнить науку с библиотекой, которая должна непрерывно расширяться; но библиотекарь располагает для своих приобретений лишь ограниченными кредитами; он должен стараться не тратить их понапрасну. Такая обязанность делать приобретения лежит на экспериментальной физике, которая одна лишь в состоянии обогащать библиотеку. Что же касается математической физики, то её задача состоит в составлении каталога. Если каталог составлен хорошо, то библиотека не делается от этого богаче, но читателю облегчается пользование её сокровищами" [5, с.93].
Вопрос о соотношении теории и опытных данных, оказавшийся в центре методологических концепций позитивизма, включая современный постпозитивизм, не является изначальным для теории познания. Фундаментальный характер имеет проблема взаимоотношения теории и реальности, хотя та или иная методология может уклоняться от её прямой постановки и явочным порядком принимать отказ от объективного значения теории, либо же наоборот, принимать идею объективной реальности, отражаемой в теории. Позитивизм, прогнавший метафизику, изгнал объективную реальность с горизонта методологии и теории познания, хотя последовательно и до конца такую позицию в теории познания проводили лишь профессиональные философы классического периода, в частности, Д. Юм и И. Кант. Естествоиспытатели, ставшие на позиции позитивизма, чаще всего двойственны в своих гносеологических представлениях, поскольку наука, обращённая к познанию природы, всегда оставляет в своём арсенале (хотя бы и "в глубине души") идею объективной истины, идею объективного смысла теории, даже если в теоретико-познавательных рассуждениях заявляет категорический отказ от всякой объективности философского плана или, как говорят в таком случае, от всякой метафизики.
Непоследовательность такого рода имеется и в философских сочинениях А. Пуанкаре, хотя в теории познания он последовательно развивает идею конвенционализма. Суть последней в том, что теория рассматривается как соглашение (конвенция), принимаемое по поводу опытных данных, но ни ложное, ни истинное по самой своей сути. Для теории сохраняется логическая правильность и другие формальные атрибуты, но не истинность в традиционном объективистском плане. Однако конвенционализм такого рода не имеет в виду, что теория является продуктом субъективного произвола отдельного исследователя. Соглашение как бы навязывается научному мышлению самой логикой познавательного процесса, в частности, соображениями удобства и простоты. Тем самым конвенция наполняется некой объективностью, идущей от познавательного процесса (но не от объективной реальности), что никоим образом не разрушает гносеологических оснований конвенционализма в рассмотренном нами смысле.
Двойственность позиции А.Пуанкаре обнаруживается в том, что он включает в контекст “объективную реальность” отношений. Теория всё-таки оказывается наделённой объективным значением, но эта объективность имеет своеобразный характер. Великий математик полагал, что теория не способна отразить природу вещей, но она отображает отношения вещей через соотношение математических символов в уравнениях математической физики: "Уравнения выражают отношения, и если уравнения остаются справедливыми, то это означает, что и эти отношения сохраняют свою реальность. Теперь, как и раньше, уравнения Френеля показывают нам наличие такого-то соотношения между одной вещью и некоторой другой вещью: только то, что мы прежде называли движением, теперь называется электрическим током. Но названия эти были просто образными выражениями, мы подставляли их вместо реальных предметов, которые природа навсегда утаила от нас. Истинные отношения между этими реальными предметами представляют собой единственную реальность, которую мы можем постигнуть; единственное условие состоит в том, чтобы те же самые отношения имели место как между этими реальными предметами, так и между образными выражениями, которыми пришлось их заместить. Раз отношения нам известны, то уже не существенно, какое образное выражение мы считаем удобным применить" [5, с.102].
Термины "вещь" и "отношение вещей" не вполне уместны в пределах той гносеология, которую развивал великий математик. Правильнее было бы говорить о данных опыта, фиксированных в чувственной форме. Употребление термина "вещь" как бы прорывает позитивистское понимание опыта и вынуждает вводить “метафизические представления”, т.е. говорить о том, что стоит за чувственным опытом и даже инициирует последний. Впрочем, не будем придирчивы к нюансам употребляемой А.Пуанкаре терминологии. Драматическая двойственность его философских представлений гораздо глубже, она пронизывает его творчество своеобразной трагической нотой. С одной стороны, в философских статьях великого учёного можно прочесть следующее: "Наука состоит из одних условных положений, и своей кажущейся достоверностью она обязана единственно этому обстоятельству; научные факты и тем более законы суть искусственное творение учёного; поэтому наука отнюдь не в состоянии открыть нам истину, она может служить нам только как правило действия" [5, с.252].
С другой стороны, совершенно очевидна своеобразная установка на объективность, которая находит своё выражение в таких суждениях: "Учёный изучает природу не потому, что это полезно; он исследует её потому, что это доставляет ему наслаждение, а это даёт ему наслаждение потому, что природа прекрасна. Если бы природа не была прекрасна, она не стоила бы того, чтобы быть познанной; жизнь не стоила бы того, чтобы быть прожитой ... Я имею в виду ту более глубокую красоту, которая кроется в гармонии частей и которая постигается только чистым разумом ... именно эта особая красота, чувство гармонии мира (выделено мной - В.Ч..), руководит нами в выборе тех фактов, которые наиболее способны усилить эту гармонию, подобно тому как артист разыскивает в чертах своего героя наиболее важные, которые сообщают ему о его характере и жизни; и нечего опасаться, что это бессознательное, инстинктивно предвзятое отношение отвлечёт учёного от поисков истины ... это бескорыстное искание истины ради её собственной красоты несёт в себе здоровое семя и может сделать человека лучше [5, с.292, 293, 254].
Для нас не является принципиальным, что идея объективной истины принимает у А. Пуанкаре эстетический характер, характер гармонии мира, чувствуемой учёным. Важно то, что концепция объективной истины врывается в гносеологию Пуанкаре вопреки его собственному постулату условности научной истины, хотя и в этом вопросе его суждения не однозначны. В более ранней работе можно прочесть: "Но та гармония, которую человеческий разум полагает открыть в природе, существует ли она вне человеческого разума? Без сомнения - нет; невозможна реальность, которая была бы полностью независима от ума, постигающего её, видящего, чувствующего её. Такой внешний мир, если бы он даже и существовал, никогда не был бы нам доступен. Но то, что мы называем объективной реальностью в конечном счёте есть то, что обще нескольким мыслящим существам и могло бы быть общо всем. Этой общею стороною, как мы увидим, может быть только гармония, выражающаяся математическими законами. Следовательно, именно эта гармония и есть объективная реальность, единственная истина, которой мы можем достигнуть" [5, с.158].
Не вдаваясь в детальное рассмотрение гносеологических воззрений Пуанкаре, которые нельзя выразить плоской одномерной схемой, мы заострим внимание лишь на тех его представлениях, которые решающим образом повлияли на формирование концепции относительности Пуанкаре-Лоренца-Эйнштейна. Объяснительные физические модели, как постоянно подчеркивал французский учёный, объективной ценности не имеют. Они конвенциональны и не могут претендовать ни на истину, ни на ложь. Они легко разрушаются новыми конвенциями, что могло бы породить мысль об эфемерности познания, если бы не решающий довод, высказанный в рассуждении учёного о познании отношений. Последняя реальность, с которой имеет дело наука, по мнению Пуанкаре, это - отношения вещей и эти отношения выражаются в соотношении математических символов, т.е. в математических структурах, используемых экспериментальной наукой. Это соображение, вытекающее из всего комплекса философско-гносеологических воззрений Пуанкаре, оказывается ключевым для выдвинутого им нового понимания принципа относительности.
Обоснование нового принципа относительности выглядит у А. Пуанкаре следующим образом. Прежде всего, французский учёный деформирует классический принцип относительности Галилея - Ньютона. Физический смысл последнего он начинает связывать не столько с утверждением о независимости механических процессов от инерциального движения системы отсчёта, сколько с фактом независимости описания явления от выбора системы координат, в которой оно будет описано. При этом Пуанкаре подчеркивает, что названное условие будет выполняться в тех случаях, когда системы (одна, в которой происходит явление, другая - в которой оно описывается) практически не взаимодействуют друг с другом, т.е. явления, происходящие в одной из них, не влияют на явления, происходящие в другой. Это положение А.Пуанкаре называет принципом физической относительности: "Мы видим, таким образом, каков смысл принципа физической относительности ... Принцип этот означает, что взаимодействие двух тел стремится к нулю, когда эти тела удаляются бесконечно друг от друга. Он означает, что два удалённых друг от друга мира ведут себя так, как если бы они были независимы друг от друга" [5, с.427].
"Физическая относительность" не противоречит принципу относительности Галилея-Ньютона, но она переносит акцент на условие, при котором любые системы (а не только инерциальные) могут рассматриваться как изолированные, т.е., не взаимодействующие друг с другом. Указанный акцент в понимании физической относительности не случаен, он обусловлен тем конечным результатом, который должен быть получен. Этот результат заключается в следующем. Поскольку отношения вещей (описываемые явления) не зависят от выбора координатной системы, то и отношения математических символов, т.е. математические уравнения, описывающие эти явления, не должны измениться. Иначе говоря, А. Пуанкаре полагает, что неизменность уравнений, описывающих отношения тел, должна соблюдаться при переходе к любой координатной системе (например, вращающейся, т.е. неинерциальной) при одном ограничительном условии: системы отсчёта, к которым “прикрепляется” система координат, должны удовлетворять физической относительности. В случае инерциальных систем подобный переход описывается преобразованием Галилея. Принцип же относительности предстаёт тогда для А. Пуанкаре как “принцип относительного движения”: “Движение всякой системы должно подчиняться одним и тем же законам независимо от того, относить ли его к неподвижным осям или к подвижным, перемещающимся прямолинейно и равномерно”. [5, с.75]. На этом пути совершается смешение физической и математической стороны дела в полном соответствии с гносеологической установкой самого А. Пуанкаре. Именно таким пониманием принципа относительности воспользовался в конечном счёте Г.А. Лоренц применительно к электродинамике движущихся тел.
Как известно, переход от одной системы координат к другой не оставит без изменения уравнений, описывающих явления в конечных (интегральных) величинах, поскольку изменятся координаты и скорости тел, а в случае перехода к ускоренной системе изменятся также и ускорения. Поэтому А. Пуанкаре подчеркивал, что принцип относительности (неизменность математических уравнений, описывающих отношения вещей), применим только к дифференциальным уравнениям, но неприменим к уравнениям интегральным: "...принцип относительности применяется не непосредственно к наблюдаемым конечным уравнениям, но к уравнениям дифференциальным" [5, с.425].
Ещё раз подчеркнём, что А. Пуанкаре видит свою задачу в обосновании названного принципа для произвольных координатных систем, лишь бы они удовлетворяли "физической относительности". Но при переходе к вращающейся системе дифференциальные уравнения также изменятся, "потому что в этом случае придётся ввести в уравнения простую и составную центробежные силы" [5, с.424]. Выход он видит в том, чтобы воспользоваться дифференциальными уравнениями третьего порядка: "При таком условии принцип относительности будет применим и в этом случае: при переходе от неподвижных осей к вращающимся эти уравнения третьего порядка не изменятся" [5, с.426].
Идея относительности А.Пуанкаре может показаться достаточно очевидной и согласующейся с принципом относительности классической науки. Действительно, если системы отсчёта не взаимодействуют друг с другом и не влияют на происходящие в них процессы, а неизменные отношения тел выражаются отношениями математических символов, то эти отношения должны быть записаны в одинаковой форме в любой из этих систем. Однако в суждениях казалось бы очевидных могут скрываться далеко не очевидные обстоятельства. Так что полезно будет прислушаться к словам античного мудреца, советовавшего обнести новорожденного вокруг очага. Такой “осмотр” нового принципа относительности позволит поставить вопрос о физических границах применения требования инвариантности к уравнениям, описывающим одно и то же явление в разных системах отсчёта.
1.Поставим вопрос так: можно ли выразить отношения вещей вне их отношения к системе отсчёта? Отрицательный ответ напрашивается сам собой, он вытекает даже из гносеологической установки позитивизма, для которого вся познаваемая реальность существует только в субъективной окраске чувственного опыта, а не "сама по себе". Между тем А. Пуанкаре оставляет указанное обстоятельство без внимания. Возникающую же здесь проблему можно пояснить его рассуждением о пространственно-временных отношениях.
Анализируя возможность возвратиться в некоторую точку Парижа, например, на площадь Пантеона, Пуанкаре ставит вопрос: значит ли это, что он возвращается в ту же самую точку пространства? Ответ самого математика заключается в следующем: "Если я говорю: "я буду здесь завтра", то, как мы видели только что, я не хочу этим сказать, что я буду завтра в той же точке пространства, где и сегодня; я имею ввиду, что буду завтра на том же расстоянии от Пантеона, что и сегодня. Но, строго говоря, и эта формулировка недостаточно ясна. Я собственно, должен был сказать: "Завтра, как и сегодня, расстояние от меня до Пантеона составят столько-то раз взятую длину моего тела" [5. с.339].
Ответ Пуанкаре приемлем, если иметь в виду возможность возвратиться в ту же самую точку мирового (абсолютного) пространства, т.е. пространства, определяемого совокупностью небесных тел, "ибо в течение этого времени Земля будет двигаться, унося с собой и площадь Пантеона, которая пробежит таким образом свыше двух миллионов километров ... но Солнце перемещается относительно Млечного пути, а Млечный путь в свою очередь, несомненно имеет движение, скорости которого мы не можем знать" [5, с.338]. Однако можно в любое время возвратиться в ту же самую точку пространства, связанного с поверхностью Земли. Но Пуанкаре противится и такой постановке вопроса, поскольку она вступает в противоречие с его идеей о том, что понятие "пространство" обозначает комплекс взаимосвязанных движений органов человеческого тела (или ощущений, вызываемых движением).
Подход Пуанкаре к происхождению понятия "пространство" базируется на том, что ощущения человека позволяют ему измерить расстояние между своим телом и внешним объектом, имеющим свойства твёрдого тела, или восстановить относительное расстояние между собой и этим телом. Понятно в этой связи утверждение математика, что "система координатных осей, к которым мы естественно относим все внешние предметы - это система осей, неизменно связанная с нашим телом, которую мы и носим всюду с собой" [5, с.190]. Но такое представление об идее пространства слишком субъективно. Если представить себе, что субъект может измерить только относительное расстояние между собой и внешним объектом, то он не сможет получить пространственную картину расположения объектов, а ограничится лишь множеством конкретных расстояний, изменяющихся с перемещением самого субъекта. В действительности же пространственная картина появляется лишь тогда, когда расстояния между телами определённым образом упорядочены, что достигается отнесением этих расстояний к неподвижной системе отсчёта, представленной группой тел, неподвижных друг относительно друга.
Последнее обстоятельство достаточно очевидно и находит свое выражение, например, в пользовании географической картой, дающей пространственную картину расположения объектов и обеспечивающей свободу выбора маршрута и определённую гарантию его правильности. Но тогда приходится признать, что пространственные отношения суть некоторая объективная реальность (даже и без абсолютной неподвижной системы отсчёта), которую субъект "ощупывает" и воспроизводит, а система отсчёта оказывается своеобразным инструментом выявления пространственных отношений тел. Такими представлениями пользуется естествознание в своей практике, с таких позиций и сам А. Пуанкаре говорит о движении Земли, Солнца и Млечного пути. Но эта естественнонаучная позиция не соответствует позитивистско-конвенционалистской гносеологии учёного и ради спасения основной гносеологической идеи возникает мучительная двойственность его суждений. Суть её в том, что пространственные отношения тел могут быть определены только путём отнесения их к системе отсчёта, в которой зафиксированы их текущие координаты, а это обстоятельство ставит под сомнение гносеологический тезис, утверждающий что отношения вещей, как главный итог познания, могут быть фиксированы безотносительно к системе отсчёта, словно бы взятые "сами по себе".
Между тем, уравнения, описывающие явления, не могут в принципе избежать величин, характеризующих отношение тел к системе отсчёта, т.е. величин, определяемых именно в этой системе. Это касается не только пространственного положения тел, но и таких характеристик как ускорение, масса, напряжённость поля (сила) и т.п. Если бы дело обстояло иначе, т.е. можно было бы фиксировать отношения вещей "сами по себе", вне отношения тел к системе отсчёта, то математическая задача перехода от одной системы к другой потеряла бы смысл. Пространственные отношения тел, которые сами по себе не изменяются от описания их в произвольной системе координат, явно или неявно вошли в уравнения, так сказать, зашифрованы в них и предстают в явном виде после решения соответствующих уравнений. Но значит ли это, что существование неизменных пространственных отношений, по-разному фиксируемых в различных системах координат, должно обязательно сопровождаться инвариантностью уравнений, описывающих динамику тел? В этом вопросе соединяются математическая и физическая задача и над его решением не должна довлеть та или иная гносеологическая догма.
2.Одним из оснований концепции относительности А.Пуанкаре является произвольность в выборе системы отсчёта, в которой описывается "отношение вещей". Великий математик стремился придать своей идее относительности статус универсального научного принципа, т.е. распространить его на любые системы отсчёта, достаточно удалённые от группы взаимодействующих тел (физическая относительность). О преодолении трудности, возникающей при переходе к ускоренной системе, уже говорилось (уравнения третьего порядка). Однако допустим ли произвол в выборе системы отсчёта при описании явлений?
Ответ на этот вопрос уже дан в первой статье. Экспериментальная наука соотносит описание явления в той или иной системе с опытными данными, полученными в ней. Последнее означает, что величины, входящие в уравнения, должны быть измерены в системе, к которой отнесены уравнения и только таким путём математические уравнения приобретают физический смысл. Например, когда мы описываем движение тел в системе отсчёта, связанной с поверхностью Земли, то должны иметь дело с реальными импульсами земных тел по отношению к массивному телу, с которым связана система координат. Формально мы могли бы выбрать для описания систему координат, связанную с движущейся велосипедной коляской, что заставит приписать Земле громадный импульс по отношению к коляске. Но как только мы захотим убедиться в существовании этого импульса путём, например, торможения Земли, то обнаруживается, что относительное движение коляски и Земли прекращается тормозящим импульсом, пропорциональным массе и скорости коляски. Громадного импульса Земли мы не обнаружим, его просто нет в реальности (он был на бумаге). Какие-то физические причины привели в движение коляску, но в рассматриваемой системе отсчёта не было сил, заставивших Землю изменить свое состояние и придти в движение относительно покоящейся коляски.
Этот пример вновь обнаруживает те же самые обстоятельства, о которых шла ранее речь при рассмотрении физического статуса картины движения небесных тел, наблюдаемой из вращающегося кресла. Суть этих обстоятельств сводится к тому, что выбор системы отсчёта для опытно-теоретического описания явлений не бывает полностью произвольным. Он определяется совокупностью физических связей предметов и задачей адекватно отобразить эти связи и взаимоотношения. Произвольными могут быть системы координат, связываемые с любым произвольным телом (велосипедной коляской или вращающимся креслом). Следствием использования такой координатной системы будет появление эфемерных величин, существующих лишь как вспомогательные математические величины в координатной, но не в физической системе. Экспериментально оправданная система для описания движений в условиях Земли или для описания объектов небесной сферы всегда будет предопределена физическими связями и соотношениями, имеющими характер объективной реальности, выявляемой исследователем.
3.Третье замечание носит гносеологический характер и касается суждения А. Пуанкаре о целях и результатах познания. С философско-гносеологической стороны с принципом относительности А. Пуанкаре можно согласиться только в том случае, если мы примем его постулат, что объектом познания являются отношения вещей, отображаемые через соотношения математических символов. Одна из рассмотренных слабостей этого утверждения лежит на поверхности. Строго говоря, не отношения вещей, а отношения физических величин отражаются в уравнениях математической физики. Точнее сказать, в уравнениях математической физики отображаются взаимосвязи и взаимоотношения физических величин, причём необходимым условием познания этих взаимоотношений является фиксация их в системе, которая, как только что указывалось, предопределена реальными взаимоотношениями тел, характеристиками которых являются физические величины.
В философском плане не менее важным является внешне скрытый, ускользающий от неподготовленного читателя контекст постулата о познании отношения вещей через отношение математических символов. Такая гносеологическая посылка неявно имеет в виду, что есть некая абсолютная (независимая от субъекта) реальность в виде отношения вещей, изоморфно представленная отношением математических символов. Этот самый абсолют предстаёт как нечто безотносительное к системе отсчёта, к самому наблюдателю и его экспериментально-измерительным процедурам. Такое видение уместно в математике и неудивительно, что у А.Пуанкаре появляется стимул заимствовать идеи топологии, в частности, понятия как "группа" и "инвариант" и перенести их в область теоретической физики. В математическом плане этот перенос по-своему эффективен. Однако применимость указанных понятий в арсенале физики резко ограничивается, во-первых, тем, что не каждая координатная система является физической системой отсчёта, и, во-вторых, тем, что переход от одной координатной системы к другой в случае неизолированных систем, с которыми они связаны, означает фактически перенос явления из одной физической системы в другую. Это значит, что физический процесс оказывается в новых условиях, изменяющих само соотношение величин.
В конечном счёте идея относительности, выдвинутая А. Пуанкаре, возникла на математической почве, дополненной гносеологическими соображениями позитивизма. Инвариантная форма записи уравнений, являющаяся практическим результатом этой идеи - формальный приём, возведённый в ранг общенаучного принципа. Его некритическое использование неизбежно ведёт к искусственным формальным построениям, отождествление которых с реальностью влечёт за собой искажение принципов экспериментальной науки ради удобства математического формализма, что и проявилось в специальной и общей теории относительности.
Необходимо всё-таки отметить, что сам А. Пуанкаре не создавал ту упрощённую гносеологическую модель “реальности по отношению”, которая сформировалась при “офизичивании” релятивистской кинематики. Но надо признать и тот факт, что французский учёный создал все условия для её появления своей позитивистской гносеологией, пренебрежением к физическим моделям как вспомогательным гипотезам конвенциального характера, и гипертрофированием роли математических структур в познании. Неудивительно, что его принцип относительности применён к решению задачи, условия которой далеки от физической относительности даже в том понимании, которое вкладывал в неё сам А. Пуанкаре.
Величины, использование которых навязано формальным приёмом, а не природой описываемого процесса, легко обнаруживают свой вспомогательный характер при попытке дать им физическую интерпретацию. В специальной теории относительности это обстоятельство проявилось в неоднократно отмечавшихся затруднениях, возникающих на пути отождествления преобразования Лоренца со свойствами пространства и времени.
Канонические правила релятивистской кинематики представлены операциями сравнения отрезков длины и промежутков времени на основе принятого преобразования. Формальные следствия указанной процедуры многократно описаны и наша задача состоит в том, чтобы рассмотреть физическую осуществимость процедур, фиксирующих релятивистские эффекты, т.е. принципиально доказать существование последних "физическими средствами для наблюдателя, не движущегося вместе с телом", как это утверждалось в высказывании А.Эйнштейна [7, с.187].
Как известно, для инерциальных систем, совершающих поступательное движение вдоль оси![]() , преобразование записывается в виде
, преобразование записывается в виде
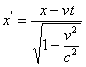 ;
; 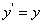 ;
; 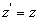 ;
; 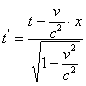 ; (1)
; (1)
при этом штрихованные координаты принадлежат системе, принимаемой за движущуюся. На основе принятого преобразования проведём анализ пространственно-временных измерений релятивистской кинематики.
Движущийся отрезок может быть измерен в сопутствующей системе прикладыванием масштаба. При этом длина отрезка движущейся системы получит значение ![]() . В покоящейся системе по правилам релятивистской кинематики она будет иметь другое значение, полученное другим способом измерения, суть которого в одновременной фиксации концов движущегося отрезка в покоящейся системе и в измерении расстояния между полученными отметками прикладыванием масштаба. Это значит, что при использовании преобразования (1) для подсчёта координат
. В покоящейся системе по правилам релятивистской кинематики она будет иметь другое значение, полученное другим способом измерения, суть которого в одновременной фиксации концов движущегося отрезка в покоящейся системе и в измерении расстояния между полученными отметками прикладыванием масштаба. Это значит, что при использовании преобразования (1) для подсчёта координат ![]() ,
, ![]() необходимо принимать одно и то же значение времени покоящейся системы
необходимо принимать одно и то же значение времени покоящейся системы ![]() . Тогда
. Тогда
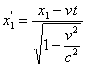 ;
; 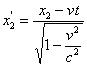 ;
;
или
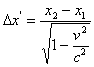 ; т.е.
; т.е. 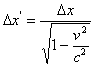 или
или ![]() (2)
(2)
Для движущегося отрезка, измеренного в покоящейся системе, получено значение длины ![]() меньшее, нежели значение
меньшее, нежели значение ![]() , полученное при измерении его прикладыванием масштаба в движущейся (сопутствующей) системе. Этот результат истолковывается как сокращение движущегося отрезка6.
, полученное при измерении его прикладыванием масштаба в движущейся (сопутствующей) системе. Этот результат истолковывается как сокращение движущегося отрезка6.
Понятно, что при всех этих измерениях с отрезком "самим по себе" ничего не происходит. Его никто не растягивает и не сжимает. Просто он измеряется разными способами, которые, согласно преобразованию Лоренца, должны давать различные результаты. По этой причине последовательный релятивизм снимает вопрос о длине отрезка "самого по себе" и считает правомерным говорить о длине лишь в отношении к процедурам измерения. Последовательное проведение такой гносеологической позиции должно вообще-то приводить к более сильному утверждению, что и стержня как такового (самого по себе) нет, что он существует лишь в отношении (если стержень существует независимо от операции измерения, то и его протяженность должна рассматриваться как нечто объективное, т.е. независимое от операций измерения, а не создаваемое в них).
Оставим однако вопрос о сути такой философской позиции. Зададимся вопросом: возможно ли физически с помощью приборов, используемых при пространственных измерениях, получить результаты, соответствующие правилам релятивистской кинематики? Они оказывается возможными только в том случае, если в движущейся системе сам собой появится (или будет принят) другой темп (ритм) времени по отношению к покоящейся и появится местное время, а вместе с ним и относительность одновременности, навязываемая преобразованием Лоренца. Если эти временные изменения физически реализуемы, то можно утверждать и физическую реализуемость релятивистской кинематики в целом. Однако реализуемы ли они? Ведь в вопросе о ходе времени и местном времени нельзя прибегнуть к той релятивности, которая оказалась палочкой-выручалочкой при сравнении отрезков, поскольку признание замедления часов движущейся системы нельзя совместить с одновременным замедлением часов покоящейся системы. Окончательный выбор (или крах попыток физической интерпретации преобразования) здесь неизбежен.
Для проверки эмпирической обоснованности преобразования времени по правилам Лоренца необходимо предварительно задать экспериментальные процедуры измерения времени, с которыми будут сопоставляться результаты преобразования. В релятивистской кинематике промежутки времени как в движущейся, так и в покоящейся системе отсчёта предполагается определять по показаниям синхронно идущих часов, расположенных в разных (в принципе во всех) точках системы отсчёта. Синхронизация осуществляется сигналом покоящегося источника света. Заметим, что при рассмотрении релятивистских эффектов времени приходится иметь дело с показаниями "одноместных" и "разноместных" часов, т.е. иметь дело с показаниями часов, находящихся в одной и той же точке системы координат, и с показаниями часов, находящихся в разных точках этой системы. Правила Лоренца предполагают различные варианты сопоставления промежутков времени при измерении последних в движущейся и покоящейся системах.
Промежуток времени 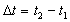 замерен по часам, расположенным в разных точках покоящейся системы
замерен по часам, расположенным в разных точках покоящейся системы ![]() и
и ![]() . Согласно преобразованию Лоренца этот промежуток времени примет в движущейся системе значение
. Согласно преобразованию Лоренца этот промежуток времени примет в движущейся системе значение
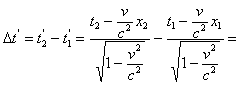
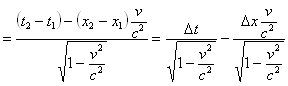 ;
;
Заметим, что в общем случае промежуток времени движущейся системы складывается из "ускорения" хода часов движущейся системы 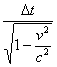 и поправки на местное время
и поправки на местное время 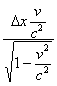 , работающей против ускорения хода часов движущейся системы.
, работающей против ускорения хода часов движущейся системы.
Промежуток времени определяется в покоящейся системе по показаниям одноместных часов, помещённых в точке ![]() .
.
Тогда 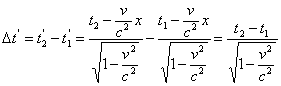 ;
; 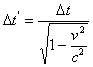 или
или ![]() .
.
Выходит (как и для отрезков), что больший промежуток времени ![]() движущейся системы отобразится в меньший промежуток времени
движущейся системы отобразится в меньший промежуток времени ![]() при его измерении в покоящейся системе.
при его измерении в покоящейся системе.
Физически это должно было бы означать, что часы движущейся системы идут быстрее вопреки распространённому утверждению о замедлении часов движущейся системы. Этот случай в релятивистской литературе обычно не анализируется.
Промежуток времени ![]() измерен по разноместным часам покоящейся системы, размещённым в точках
измерен по разноместным часам покоящейся системы, размещённым в точках ![]() и
и ![]() . Определим
. Определим ![]() при условии, что
при условии, что ![]() . Эту операцию принято рассматривать как сопоставление одноместных движущихся часов с разноместными покоящимися.
. Эту операцию принято рассматривать как сопоставление одноместных движущихся часов с разноместными покоящимися.
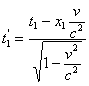 ;
; 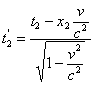 ;
; 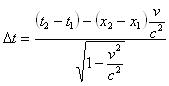 , т.е.
, т.е. 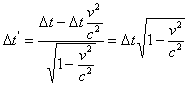 .
.
Промежуток времени движущейся системы ![]() (показания движущихся часов) оказывается меньше промежутка времени
(показания движущихся часов) оказывается меньше промежутка времени ![]() покоящейся системы (показания покоящихся часов), что истолковывается как отставание (замедление) движущихся часов.
покоящейся системы (показания покоящихся часов), что истолковывается как отставание (замедление) движущихся часов.
Процедуры (II) и (III) дают частные случаи преобразования временных промежутков, но в них есть нечто общее. Эмпирическая интерпретация процедуры (II) должна означать, что одни и те же покоящиеся часы сопоставляются с двумя синхронно идущими движущимися часами. Тогда отстают одноместные покоящиеся часы. В случае (III) одноместные движущиеся часы сопоставляются с двумя разноместными покоящимися часами и теперь отстают одноместные движущиеся часы. Промежуток времени на одноместных часах всегда оказывается короче, чем на идущих синхронно разноместных часах, независимо от того, какие из них считать движущимися, а какие покоящимися.
Это обстоятельство само по себе уже свидетельствует об искусственности и эфемерности так называемого замедления хода часов. Попытка "офизичить" это замедление ведёт к неразрешимому противоречию. Пусть замедлились одноместные движущиеся часы. Но в своей системе они идут синхронно с другими часами, расположенными в разных точках системы отсчёта. Значит, ход времени движущейся системы замедлился по отношению к ходу времени покоящейся системы, иначе все наши рассуждения вообще потеряют смысл. Но в то же время, ничего не изменяя в самой ситуации, мы должны утверждать, что замедлились одноместные часы покоящейся системы, которые включены в синхронно идущий комплекс часов покоящейся системы, т.е. мы должны утверждать, что ход времени покоящейся системы замедлился по отношению к ходу времени движущейся системы. Противоречие очевидное и неизбежное. На него неоднократно обращали внимание уже в первое десятилетие после появления специальной теории относительности. Однако оно нисколько не поколебало приверженцев релятивизма. Более того, в теории относительности несложный кунштюк преобразования времени, выполняемый в третьем варианте, окутывается магическими интеллектуальными пассами и выдается за проникновение в сокровенные глубины Вселенной. Невольно вспоминается в этой связи мудрое предостережение, адресованное в свое время великому Кеплеру: ни с чем несообразно, чтобы действительность незамедлительно приспособлялась к придуманным каждым магистром гипотезам.
Указание на неразрешимое противоречие, возникающее при попытке соединить результаты преобразования времени с экспериментальными процедурами, предполагаемыми самой релятивистской кинематикой, ставит точку над рассмотрением её физической обоснованности. Однако анализ формальных следствий преобразования Лоренца будет неполным, если мы оставим без внимания так называемое "местное время". Попытку придать ему физический смысл, т.е. представить последнее как величину, которую можно зафиксировать приборами, никто не предпринимал, хотя достаточно было упрёков в адрес Г.А. Лоренца за то, что он считал местное время фиктивной величиной. Но странный фокус релятивистики в том и заключается, что с местным временем считаются при вычислениях, в то время как оно нигде не существует и не наблюдается.
Намерение представить местное время как физическую величину, поддающуюся измерению приборами, оказывается бесплодным. В покоящейся системе часы покоящегося наблюдателя идут синхронно и никакого местного времени в его системе нет. Но точно также обстоит дело и для движущегося наблюдателя, иначе пришлось бы отказаться от принципа относительности и эквивалентности систем отсчёта. Используя свои приборы, наблюдатели в своих системах отсчёта местного времени не обнаружат. Однако, если мы запретим наблюдателям пользоваться своими синхронно идущими часами и заставим их вычислять промежутки времени по правилам Лоренца, то тотчас появится местное время как вычислительная операция. Это легко показать на примерах вычисления в случаях (II) и (III). В случае (II) в покоящейся системе местное время отсутствует по определению, а поправка 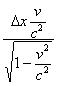 для движущейся системы определяется разностью координат покоящихся часов, по которым брал отсчёт покоящийся наблюдатель. Поскольку эта разность равна 0 (часы одноместные), то и в движущейся системе местного времени нет и, как было показано для случая (II), движущиеся часы опережают покоящиеся.
для движущейся системы определяется разностью координат покоящихся часов, по которым брал отсчёт покоящийся наблюдатель. Поскольку эта разность равна 0 (часы одноместные), то и в движущейся системе местного времени нет и, как было показано для случая (II), движущиеся часы опережают покоящиеся.
Для случая (III) промежуток времени определялся по показаниям синхронно идущих разноместных покоящихся часов. Отставание одноместных движущихся часов в случае (III) обусловлено именно поправкой на местное время, а не замедлением темпа, который согласно (II) должен возрасти. Как указывалось, в движущейся системе промежуток времени составит 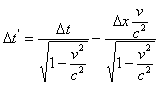 ;
;
Отставание возникает из суммы ускорившегося темпа хода движущихся часов 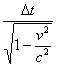 и поправки на местное время
и поправки на местное время 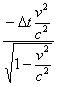 . При условии
. При условии ![]() эта поправка
эта поправка 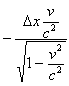 . Общий итог выразится известным результатом
. Общий итог выразится известным результатом ![]() .
.
При попытке обосновать этот результат измерениями окажется, что в покоящейся системе местного времена нет по определению (здесь часы идут синхронно, а процедура синхронизации поправки на местное время не предполагает), а движущийся наблюдатель не должен обращаться к местному времени потому, что он пользуется одноместными часами. Тем не менее, поправка на местное время все же появляется, но не как показание приборов, способных её зафиксировать, а как вычислительный приём. Нигде не существующее и не наблюдаемое в принципе местное время появляется, чтобы обеспечить "отставание" одноместных часов по отношению к разноместным.. Поскольку мы познакомились с формально-математической природой принципа относительности Пуанкаре-Лоренца, то для нас природа местного времени не составляет тайны. Оно есть фиктивная величина, тот самый Deus ex machine, который явился, чтобы обеспечить достижение формального результата, появление которого предполагается правилами игры (инвариантной записью уравнений Максвелла).
Невозможность физически реализовать систему измерений, удовлетворяющую преобразованию Лоренца, делает вполне очевидной математическую условность преобразования времени, как и математическую условность преобразования Лоренца в целом. Принятые в релятивистской кинематике представления об относительности одновременности и о замедлении времени движущейся системы, позволяющем путешествующему космонавту намного пережить своих сверстников, являет собой странную смесь противоестественной фантасмагории, приписывающей реальности чудодейственные свойства, с одновременным позитивистским указанием на эфемерность и относительность этих эффектов ("реальность по отношению").
Формальный характер преобразования легко обнаруживается при рассмотрении общего случая (I) сопоставления промежутков времени. Как указывалось, промежутки времени преобразуются по формуле 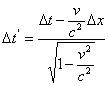 , где
, где ![]() независимая переменная, не являющаяся функцией
независимая переменная, не являющаяся функцией ![]() . Один и тот же промежуток времени
. Один и тот же промежуток времени ![]() при одной и той же относительной скорости систем можно фиксировать разными парами часов покоящейся системы и в зависимости от расстояния между ними для неизменного
при одной и той же относительной скорости систем можно фиксировать разными парами часов покоящейся системы и в зависимости от расстояния между ними для неизменного ![]() будут получаться разные интервалы
будут получаться разные интервалы ![]() в движущейся системе. Последнее обстоятельство показывает, что местное время не есть принадлежность движущейся системы. Оно появляется в ней по произволу покоящегося наблюдателя в зависимости от того, на какие часы в своей системе он "посмотрел". Придать какой-либо физический смысл этому факту вообще не предоставляется возможным.
в движущейся системе. Последнее обстоятельство показывает, что местное время не есть принадлежность движущейся системы. Оно появляется в ней по произволу покоящегося наблюдателя в зависимости от того, на какие часы в своей системе он "посмотрел". Придать какой-либо физический смысл этому факту вообще не предоставляется возможным.
Поскольку идея инвариантности привнесена А.Пуанкаре из раздела топологии, то геометрическая интерпретация преобразования Лоренца является наиболее простым и естественным средством выявления его топологического смысла. Преобразование Лоренца позволяет описывать квадратным уравнением сферы одну и ту же поверхность в различных системах отсчёта, причём центр сферы покоящейся системы не будет совпадать с центром той же самой поверхности, принимаемым в движущейся системе (рис.3).
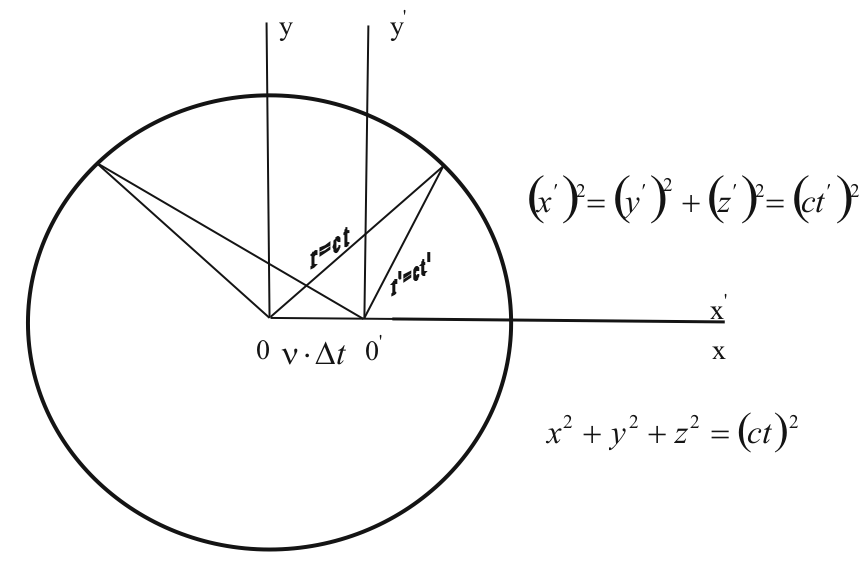
Рис.3.
В покоящейся системе поверхность сферы задана уравнением ![]() , т.е. радиус сферы
, т.е. радиус сферы ![]() . Выберем некоторое фиксированное значение
. Выберем некоторое фиксированное значение ![]() и попробуем поверхность той же самой сферы описать квадратным уравнением в штрихованной системе имея ввиду, что “центр сферы” совпадает с точкой 0' - началом координат штрихованной системы. Нетрудно видеть, что радиус такой "сферы" не будет постоянным. Величина радиуса задается преобразованием Лоренца
и попробуем поверхность той же самой сферы описать квадратным уравнением в штрихованной системе имея ввиду, что “центр сферы” совпадает с точкой 0' - началом координат штрихованной системы. Нетрудно видеть, что радиус такой "сферы" не будет постоянным. Величина радиуса задается преобразованием Лоренца
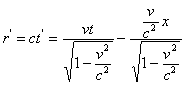 . При условии, что
. При условии, что ![]() можно подобрать такие функция для
можно подобрать такие функция для ![]() ,
, ![]() ,
, ![]() , что все точки поверхности в штрихованной системе координат будут связаны с её “центром” квадратным уравнением "сферы". В зависимости
, что все точки поверхности в штрихованной системе координат будут связаны с её “центром” квадратным уравнением "сферы". В зависимости ![]() от скорости, времени и координаты, полученной как формальный приём аналитической геометрии, заключён весь глубокий смысл релятивистского единства пространства и времени, по поводу которого сказано столько прочувствованных фраз.
от скорости, времени и координаты, полученной как формальный приём аналитической геометрии, заключён весь глубокий смысл релятивистского единства пространства и времени, по поводу которого сказано столько прочувствованных фраз.
Релятивистская кинематика - пример глубокомысленной философии на мелком месте. Прямого физического смысла, который ей обычно приписывается, она не имеет, и рассуждение о существующем якобы в физической реальности замедлении движущихся часов является внушённой и внушаемой иллюзией, независимо от того, сознательно или неосознанно она поддерживается. Отношение инвариантности здесь принудительно перенесено на характеристики электромагнитного процесса и в угоду математическому формализму деформированы исходные понятия, чем создана иллюзия решения проблемы. Нет особой необходимости останавливаться на формальной условности второго постулата СТО, так и не получившего (и не могущего получить) серьёзного экспериментального подтверждения. Этому соглашению можно подчинить свои вычисления, но ему никогда не подчинялись природные явления. Впрочем, в связи с разработкой лазерного космического оружия можно быть уверенным, что эта истина быстро и с необходимостью будет осознана, поскольку скорости мишени и лазерного импульса придется складывать по классическому правилу. Е.Уоллес указывает на вероятность того, что "военные США считают относительную скорость света в космосе ![]() сверхсекретной информацией" [6, с.3].
сверхсекретной информацией" [6, с.3].
1. Тело покоится или совершает равномерное прямолинейное движение, если на него не действует сила - утверждает закон инерции. То же самое, но "от противного" утверждает принцип относительности: если система покоится или совершает равномерное прямолинейное движение, то отсутствуют какие-либо силы, вызванные этим движением и влияющие на состояние тел системы. Единственное условие - системы должны быть изолированными, т.е. двигаться в пустоте, дабы не возникали побочные эффекты, вызванные равномерным движением (эфирный ветер, воздушный поток и т.п.).
2. А.Эйнштейн в более поздней своей работе так формулирует второй постулат СТО: "Один и тот же световой луч распространяется в пустоте со скоростью С не только в системе отсчёта К, но и в каждой другой системе К', движущейся равномерно и прямолинейно относительно К". [8, с.367]. Конвенциональность этой формулировки можно уяснить из рассмотрения следующего мысленного эксперимента (рис.2).
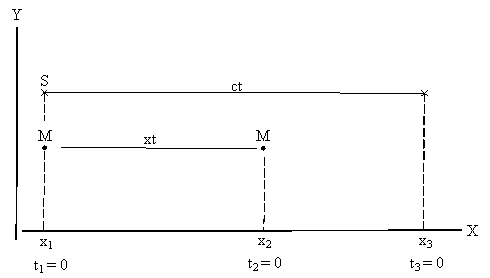
Рис.2.
Пусть в момент ![]() , когда тело М проходит координату
, когда тело М проходит координату ![]() , покоящийся источник S с координатой
, покоящийся источник S с координатой ![]() испускает световой сигнал. В момент
испускает световой сигнал. В момент ![]() световой импульс и тело М будут иметь координаты
световой импульс и тело М будут иметь координаты ![]()
![]()
![]() . Расстояние
. Расстояние ![]() , т.е. относительное смещение тела М и фронта светового импульса, измеренное в нашей покоящейся системе К, будет определяться их относительной скоростью
, т.е. относительное смещение тела М и фронта светового импульса, измеренное в нашей покоящейся системе К, будет определяться их относительной скоростью ![]() . Однако, если мы свяжем с телом М координатную систему, то по релятивистским условиям должны принять (опытом это не навязывается), что относительная скорость тела М и светового импульса равна
. Однако, если мы свяжем с телом М координатную систему, то по релятивистским условиям должны принять (опытом это не навязывается), что относительная скорость тела М и светового импульса равна ![]() . Движущийся наблюдатель может выполнить это требование только за счёт изменения единиц измерения. При этом для торжества релятивистской кинематики необходимо запретить покоящемуся наблюдателю использовать классическое правило сложения скоростей при определении относительной скорости тела и фронта светового импульса, а заодно и запретить физический эксперимент по определению этой скорости.
. Движущийся наблюдатель может выполнить это требование только за счёт изменения единиц измерения. При этом для торжества релятивистской кинематики необходимо запретить покоящемуся наблюдателю использовать классическое правило сложения скоростей при определении относительной скорости тела и фронта светового импульса, а заодно и запретить физический эксперимент по определению этой скорости.
3. В противном случае никакого принципа не требуется, так как инвариантность достигается автоматически, как это было с дифференциальными уравнениями Ньютона. Неудивительно, что за два века существования классической физики вплоть до постановки задачи электродинамики движущихся тел никто не придавал никакого значения признаку инвариантности уравнений Ньютона относительно преобразования Галилея.
4. Нет фатальной неизбежности видеть в преобразовании Лоренца единственно возможное средство решения задачи. Одна из причин фетишизации этого приёма состоит в том, что ему не были активно противопоставлены альтернативные пути, в частности, поиск уравнений, описывающих поле в движущейся системе с учётом его "деформации", вызванной относительным движением систем. Указанная “деформация” должна зависеть от относительной, а не абсолютной (эфирной) скорости движения системы (по этому пути направлялся В.Ритц). Такой путь связан с построением физической модели, объясняющей природу поля, и он не требует, чтобы эффекты, возникающие при относительном движении неизолированных систем, объяснялись причинами, имеющими эфемерно-конвенционалистскую природу.
5. В работе Логунова сказано также, что "уравнения механики остаются форминвариантными при преобразовании Галилея, а, следовательно (выделено мной - В.Ч.) для всех механических процессов выполняется принцип относительности" [3, с. 16]. Следует заметить, что известный учёный, следуя канону релятивистского понимания принципа относительности, поменял местами причину и следствие. В этой работе есть очень точное утверждение: "Преобразование Галилея и принцип относительности - это разные вещи" [3, с.17]. Почему бы не проявить последовательность и сказать точно также, что преобразование Лоренца и принцип относительности - разные вещи?
6. Эффект "сокращения" в релятивистской кинематике симметричен, т.е. возникает в обеих системах независимо от того, какая из них движется или считается покоящейся. Пусть по-прежнему движущейся будет штрихованная система. Но теперь длину отрезка ![]() покоящейся системы будем измерять в движущейся (штрихованной)системе. В этом случае мы должны фиксировать в движущейся системе координат концы покоящегося отрезка (точки
покоящейся системы будем измерять в движущейся (штрихованной)системе. В этом случае мы должны фиксировать в движущейся системе координат концы покоящегося отрезка (точки ![]() ,
, ![]() ) одновременно по часам движущейся системы. Для этого можно воспользоваться преобразованием в прежней форме (1), приняв при вычислениях
) одновременно по часам движущейся системы. Для этого можно воспользоваться преобразованием в прежней форме (1), приняв при вычислениях ![]() . Согласно формулам (1)
. Согласно формулам (1) ![]() ;
; ![]() . Соответственно
. Соответственно
![]() . Из уравнения
. Из уравнения ![]() следует
следует ![]() .
.
Путём соответствующей подстановки получим ![]() (3),
(3),
противоположное полученному ранее результату (2), т.е. для покоящегося отрезка ![]() получено меньшее значение длины
получено меньшее значение длины ![]() при измерении его в движущейся системе, т.е. покоящийся отрезок сокращается при измерении его в движущейся системе.
при измерении его в движущейся системе, т.е. покоящийся отрезок сокращается при измерении его в движущейся системе.
Согласовать (2) и (3) несложно, если встать на позицию последовательного релятивизма, утешающего себя тем, что эти длины получены в разных системах отсчёта и каждый наблюдатель в своей системе отсчёта будет иметь "укорочение" отрезка другой системы. При этом обнаруживается, что сокращение определяется не тем, какая из систем движется, а тем, в какой системе применяется процедура одновременной фиксации концов отрезка противоположной системы.
Последовательный релятивист может удовлетвориться мыслью, что движение относительно, что разграничение движущейся и покоящейся систем условно и что покоящейся всегда можно назвать ту систему, в которой одновременно фиксируются концы измеряемого отрезка (иначе говоря, покоящаяся система определяется не физическими обстоятельствами, а выбором ![]() или
или ![]() ). Цена этого утешения - последовательный гносеологический релятивизм, т.е. отказ от объективной реальности и подмена объективной физической ситуации правилами интеллектуальной игры. Определяя правила преобразования, два наших релятивиста договорились, что движется штрихованная система. Результаты же измерений, узаконивающие взаимные сокращения отрезков, лишают это соглашение физического смысла, и превращают его в пустую формальность. Выясняется, что единственный смысл соглашения, отождествляющего видимую картину с реальностью - определить первоначальную форму записи преобразования, которым будут пользоваться релятивисты, иначе говоря, определить правила игры. Остается объявить несуществующей длину саму по себе и довольствоваться одновременными измерениями в своей системе как единственной реальностью в полном соответствии с учением Протагора: что как кому является, так оно и есть для того, кому является. Можно ликовать по поводу столь счастливой возможности убежать от объективной реальности, но нужно безоглядно верить в релятивизм, чтобы называть эту бесхитростную интеллектуальную забаву исследованием природы или физической теорией. Впрочем, даже эти детские фокусы станут невозможными, когда мы обратимся к измерению времени и временных промежутков.
). Цена этого утешения - последовательный гносеологический релятивизм, т.е. отказ от объективной реальности и подмена объективной физической ситуации правилами интеллектуальной игры. Определяя правила преобразования, два наших релятивиста договорились, что движется штрихованная система. Результаты же измерений, узаконивающие взаимные сокращения отрезков, лишают это соглашение физического смысла, и превращают его в пустую формальность. Выясняется, что единственный смысл соглашения, отождествляющего видимую картину с реальностью - определить первоначальную форму записи преобразования, которым будут пользоваться релятивисты, иначе говоря, определить правила игры. Остается объявить несуществующей длину саму по себе и довольствоваться одновременными измерениями в своей системе как единственной реальностью в полном соответствии с учением Протагора: что как кому является, так оно и есть для того, кому является. Можно ликовать по поводу столь счастливой возможности убежать от объективной реальности, но нужно безоглядно верить в релятивизм, чтобы называть эту бесхитростную интеллектуальную забаву исследованием природы или физической теорией. Впрочем, даже эти детские фокусы станут невозможными, когда мы обратимся к измерению времени и временных промежутков.
1.Бэкон Ф. Сочинения в 2-х томах. - Т.2.-М.: Мысль,1978.
2.Ефимов А.А. О некоторых следствиях закона сохранения момента количества движения // Некоторые проблемы исследования Вселенной. - Л.,1973.-С.209-225.
3.Логунов А.А. Лекции по теории относительности и гравитации. - М.,1977.
4.Ньютон И. Математические начала натуральной философии // А.Н. Крылов. Собрание трудов. - Т.7.М.-Л.,1936.
5.Пуанкаре А. О науке.- М.: Наука, 1983.
6. Scientific ethics. V.1. 3. 1985.
7.Эйнштейн А. К парадоксу Эренфеста // Собр. науч. тр. – Т1, с.187.
8.Эйнштейн А. К проблеме относительности // Собр.науч.тр.-Т.1.-С.385-394.
9.Эйнштейн А. Краткий очерк развития теории относительности // Собр. науч. тр. - Т.2. - С.99-104.
Формат 60х84 1/16. Объём 2, 5 печ. л. Заказ 125, Цена 80 коп. Тираж 130 экз.
Малое предприятие “Полиграфист”
634055, Томск-55, пр. Академический, 2/8
Дата установки: 04.02.2007
[вернуться к содержанию сайта]